Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 100, 101, 102 sách giáo khoa Toán 11 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
a) Nếu các trường hợp có thể xảy ra đối với hai đường thẳng \(a,b\) cùng nằm trong một mặt phẳng.
a) Nếu các trường hợp có thể xảy ra đối với hai đường thẳng \(a,b\) cùng nằm trong một mặt phẳng.

b) Cho tứ diện \(ABCD\). Hai đường thẳng \(AB\) và \(CD\) có cùng nằm trong bất kì mặt phẳng nào không?
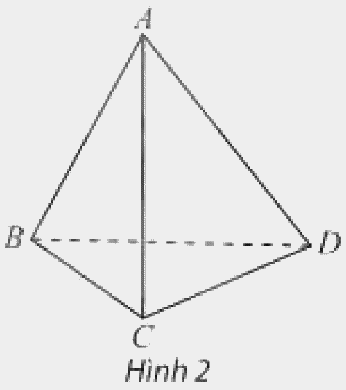
Phương pháp giải:
Quan sát hình ảnh, dựa vào vị trí tương đối của hai đường thẳng trong mặt phẳng.
Lời giải chi tiết:
a) Khi hai đường thẳng \(a,b\) cùng nằm trong một mặt phẳng thì:
‒ Nếu \(a,b\) có vô số điểm chung: Hai đường thẳng \(a,b\) trùng nhau.
‒ Nếu \(a,b\) có duy nhất một điểm chung: Hai đường thẳng \(a,b\) cắt nhau.
‒ Nếu \(a,b\) không có điểm chung: Hai đường thẳng \(a,b\) song song với nhau.
b) Hai đường thẳng \(AB\) và \(CD\) không cùng nằm trong bất kì mặt phẳng nào.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây:
a) \(AB\) và \(CD\);
b) \(SA\) và \(SC\);
c) \(SA\) và \(BC\).

Phương pháp giải:
Dựa vào vị trí tương đối của hai đường thẳng trong không gian:
• Trường hợp 1: Có một mặt phẳng chứa \(a\) và \(b\). Khi đó ta nói \(a\) và \(b\) đồng phẳng. Theo kết quả của hình học phẳng, có ba khả năng sau đây xảy ra:
‒ Nếu \(a\) và \(b\) có hai điểm chung thì ta nói \(a\) trùng \(b\).
‒ Nếu \(a\) và \(b\) có một điểm chung duy nhất M thì ta nói \(a\) và \(b\) cắt nhau tại M.
‒ Nếu \(a\) và \(b\) không có điểm chung thì ta nói \(a\) và \(b\) song song với nhau.
• Trường hợp 2: Không có mặt phẳng nào chứa cả \(a\) và \(b\). Khi đó ta nói hai đường thẳng \(a\) và \(b\) chéo nhau hay \(a\) chéo với \(b\).
Lời giải chi tiết:
a) \(AB\) và \(CD\) cùng nằm trong mặt phẳng \(\left( {ABCD} \right)\).
\(ABCD\) là hình bình hành nên \(AB\parallel C{\rm{D}}\).
b) \(SA\) và \(SC\) cùng nằm trong mặt phẳng \(\left( {SAC} \right)\).
Do đó \(SA\) và \(SC\) cắt nhau tại \(S\).
c) Giả sử \(SA\) và \(BC\) cùng nằm trong mặt phẳng \(\left( P \right)\).
Suy ra đường thẳng \(AC\) cũng nằm trong \(\left( P \right)\).
Do đó \(\left( P \right)\) chứa cả 4 điểm của tứ diện \(SABC\) (vô lí do \(S\) không nằm trong mặt phẳng \(\left( {ABCD} \right)\)).
Vậy \(SA\) và \(BC\) không cùng nằm trong một mặt phẳng. Vậy \(SA\) và \(BC\) chéo nhau.
Hãy chỉ ra các ví dụ về hai đường thẳng song song, cắt nhau và chéo nhau trong hình cầu sắt ở Hình 6.

Phương pháp giải:
Quan sát, dựa vào vị trí tương đối của hai đường thẳng trong không gian.
Lời giải chi tiết:
‒ Hai thanh sắt đối diện nhau ở hai bên cầu song song với nhau.
‒ Hai thanh sắt liền nhau cùng nằm ở thành cầu hoặc mái cầu cắt nhau.
‒ Thanh sắt nằm ở mái cầu và thanh sắt nằm ở thành cầu chéo nhau.
Mục 1 của chương trình Toán 11 tập 1 - Chân trời sáng tạo tập trung vào các kiến thức cơ bản về giới hạn của hàm số. Đây là nền tảng quan trọng để học sinh hiểu rõ hơn về đạo hàm và tích phân trong các chương tiếp theo. Việc nắm vững các khái niệm về giới hạn một bên, giới hạn tại vô cùng, và các tính chất của giới hạn là vô cùng cần thiết.
Để giải các bài tập trong Mục 1, học sinh cần nắm vững các định nghĩa và tính chất của giới hạn. Dưới đây là một số phương pháp thường được sử dụng:
Đề bài: Tính giới hạn lim (2x + 1) khi x tiến tới 3.
Lời giải: Áp dụng tính chất của giới hạn, ta có: lim (2x + 1) = 2 * lim x + lim 1 = 2 * 3 + 1 = 7.
Đề bài: Tính giới hạn lim (x^2 - 4) / (x - 2) khi x tiến tới 2.
Lời giải: Ta có thể phân tích tử thức thành (x - 2)(x + 2). Do đó, lim (x^2 - 4) / (x - 2) = lim (x + 2) = 2 + 2 = 4.
Đề bài: Tính giới hạn lim (1/x) khi x tiến tới vô cùng.
Lời giải: Khi x tiến tới vô cùng, 1/x tiến tới 0. Do đó, lim (1/x) = 0.
Khi giải các bài tập về giới hạn, học sinh cần chú ý đến các điểm sau:
Hy vọng với những hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập về giới hạn của hàm số. Chúc các em học tập tốt!