Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 62, 63, 64 sách giáo khoa Toán 11 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Hai người thợ trong hình đang thả dây dọi từ một điểm (M) trên trần nhà và đánh dấu điểm (M') nơi đầu nhọn quả dọi chạm sàn.
Hai người thợ trong hình đang thả dây dọi từ một điểm \(M\) trên trần nhà và đánh dấu điểm \(M'\) nơi đầu nhọn quả dọi chạm sàn. Có nhận xét gì về đường thẳng \(MM'\) với mặt sàn?
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
Đường thẳng \(MM'\) vuông góc với mặt sàn.
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\) và đáy \(ABCD\) là hình chữ nhật. Xác định hình chiếu vuông góc của điểm \(C\), đường thẳng \(CD\) và tam giác \(SC{\rm{D}}\) trên mặt phẳng \(\left( {SAB} \right)\).
Phương pháp giải:
Sử dụng phép chiếu vuông góc.
Lời giải chi tiết:

• Ta có:
\(\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC\\AB \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right)\)
Vậy \(B\) là hình chiếu vuông góc của điểm \(C\) trên mặt phẳng \(\left( {SAB} \right)\).
• Ta có:
\(\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
Vậy \(A\) là hình chiếu vuông góc của điểm \(D\) trên mặt phẳng \(\left( {SAB} \right)\).
Lại có \(B\) là hình chiếu vuông góc của điểm \(C\) trên mặt phẳng \(\left( {SAB} \right)\).
Vậy đường thẳng \(AB\) là hình chiếu vuông góc của đường thẳng \(CD\) trên mặt phẳng \(\left( {SAB} \right)\).
• Ta có:
\(A\) là hình chiếu vuông góc của điểm \(D\) trên mặt phẳng \(\left( {SAB} \right)\).
\(B\) là hình chiếu vuông góc của điểm \(C\) trên mặt phẳng \(\left( {SAB} \right)\).
\(S \in \left( {SAB} \right)\)
Vậy tam giác \(SAB\) là hình chiếu vuông góc của tam giác \(SCD\) trên mặt phẳng \(\left( {SAB} \right)\).
Cho đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\) và \(b\) là đường thẳng không thuộc \(\left( P \right)\) và không vuông góc với \(\left( P \right)\). Lấy hai điểm \(A,B\) trên \(b\) và gọi \(A',B'\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) trên \(\left( P \right)\).

a) Xác định hình chiếu \(b'\) của \(b\) trên \(\left( P \right)\).
b) Cho \(a\) vuông góc với \(b\), nêu nhận xét về vị trí tương đối giữa:
i) đường thẳng \(a\) và \(mp\left( {b,b'} \right)\);
ii) hai đường thẳng \(a\) và \(b'\).
c) Cho \(a\) vuông góc với \(b'\), nêu nhận xét về vị trí tương đối giữa:
i) đường thẳng \(a\) và \(mp\left( {b,b'} \right)\);
ii) giữa hai đường thẳng \(a\) và \(b\).
Phương pháp giải:
Sử dụng định lí: Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
Lời giải chi tiết:
a) Ta có: \(AA' \bot \left( P \right),BB' \bot \left( P \right),A,B \in b\)
Vậy hình chiếu vuông góc của đường thẳng \(b\) trên mặt phẳng \(\left( P \right)\) là đường thẳng \(A'B'\).
Vậy \(b' \equiv A'B'\).
b) Ta có:
\(\left. \begin{array}{l}AA' \bot \left( P \right) \Rightarrow AA' \bot a\\a \bot b\end{array} \right\} \Rightarrow a \bot mp\left( {b,b'} \right)\)
\(\left. \begin{array}{l}a \bot mp\left( {b,b'} \right)\\b' \subset mp\left( {b,b'} \right)\end{array} \right\} \Rightarrow a \bot b'\)
c) Ta có:
\(\left. \begin{array}{l}AA' \bot \left( P \right) \Rightarrow AA' \bot a\\a \bot b'\end{array} \right\} \Rightarrow a \bot mp\left( {b,b'} \right)\)
\(\left. \begin{array}{l}a \bot mp\left( {b,b'} \right)\\b \subset mp\left( {b,b'} \right)\end{array} \right\} \Rightarrow a \bot b\)
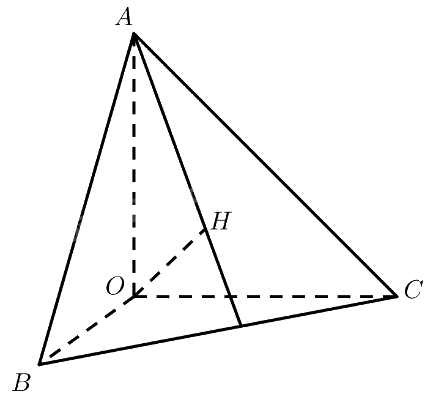
Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc. Vẽ đường thẳng qua \(O\) và vuông góc với \(\left( {ABC} \right)\) tại \(H\). Chứng minh \(AH \bot BC\).
Phương pháp giải:
Cách chứng minh hai đường thẳng vuông góc:
Cách 1: Chứng minh góc giữa chúng bằng \({90^ \circ }\).
Cách 2: Chứng minh đường thẳng này vuông góc với một mặt phẳng chứa đường thẳng kia.
Lời giải chi tiết:

\(\begin{array}{l}\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC\\OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC\\ \Rightarrow BC \bot \left( {OAH} \right) \Rightarrow BC \bot AH\end{array}\)
Nếu cách tìm hình chiếu vuông góc của một đoạn thẳng \(AB\) trên trần nhà xuống nền nhà bằng hai dây dọi.
Phương pháp giải:
Sử dụng phép chiếu vuông góc.
Lời giải chi tiết:
Thả dây dọi từ điểm \(A\) và đánh dấu điểm \(A'\) nơi đầu quả dọi chạm sàn.
Thả dây dọi từ điểm \(B\) và đánh dấu điểm \(B'\) nơi đầu quả dọi chạm sàn.
Khi đó đoạn thẳng \(A'B'\) là hình chiếu vuông góc của một đoạn thẳng \(AB\) trên trần nhà xuống nền nhà.
Mục 3 trong SGK Toán 11 tập 2 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ đi sâu vào phân tích từng bài tập trang 62, 63, 64, cung cấp lời giải chi tiết và giải thích rõ ràng từng bước thực hiện.
Bài tập này thường yêu cầu học sinh sử dụng đạo hàm để tìm cực trị, khoảng đồng biến, nghịch biến của hàm số. Để giải bài tập này, các em cần thực hiện các bước sau:
Ví dụ, cho hàm số y = x3 - 3x2 + 2. Ta có y' = 3x2 - 6x. Giải phương trình y' = 0, ta được x = 0 và x = 2. Bảng biến thiên sẽ giúp xác định hàm số đồng biến trên khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2).
Các bài toán tối ưu thường yêu cầu tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số trên một khoảng cho trước. Phương pháp giải thường bao gồm:
Ví dụ, tìm giá trị lớn nhất của hàm số y = -x2 + 4x - 3 trên khoảng [0, 2]. Ta có y' = -2x + 4. Giải phương trình y' = 0, ta được x = 2. Tính giá trị của hàm số tại x = 0, x = 2, ta được y(0) = -3 và y(2) = 1. Vậy giá trị lớn nhất của hàm số trên khoảng [0, 2] là 1.
Các bài toán thực tế thường đòi hỏi học sinh phải chuyển đổi bài toán thành một bài toán toán học và sử dụng đạo hàm để giải quyết. Ví dụ, một bài toán về tối ưu hóa diện tích hình chữ nhật với chu vi cho trước có thể được giải bằng cách sử dụng đạo hàm để tìm giá trị lớn nhất của diện tích.
Việc giải các bài tập trong mục 3 trang 62, 63, 64 SGK Toán 11 tập 2 - Chân trời sáng tạo đòi hỏi sự hiểu biết sâu sắc về đạo hàm và các ứng dụng của nó. Hy vọng rằng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.