Bài 12 trang 87 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các hàm số lượng giác cơ bản, tính chất của chúng và các phương pháp giải phương trình lượng giác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 12 trang 87, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn bằng \(2a\)
Đề bài
Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn bằng \(2a\), cạnh đáy nhỏ bằng \(a\), chiều cao \(h = 2a\) và bán kính đáy phần trụ rỗng bên trong bằng \(\frac{a}{2}\).
a) Tìm góc phẳng nhị diện tạo bởi mặt bên và mặt đáy.
b) Tính thể tích chân cột nói trên theo \(a\).
Phương pháp giải - Xem chi tiết
‒ Cách xác định góc phẳng nhị diện \(\left[ {A,d,B} \right]\): Dựng mặt phẳng \(\left( P \right)\) vuông góc với \(d\), gọi \(a,a'\) lần lượt là giao tuyến của \(\left( P \right)\) với hai nửa mặt phẳng chứa \(A,B\), khi đó \(\left[ {A,d,B} \right] = \left( {a,a'} \right)\).
‒ Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).
‒ Sử dụng công thức tính thể tích khối trụ: \(V = \pi {R^2}h\).
Lời giải chi tiết
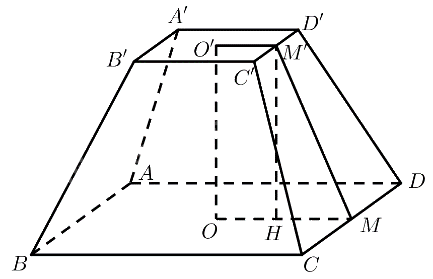
Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 2{\rm{a}},A'B' = a,OO' = 2a\).
Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'\).
\(A'B'C'{\rm{D}}'\) là hình vuông \( \Rightarrow O'M' \bot C'{\rm{D}}'\)
\(CDD'C'\) là hình thang cân \( \Rightarrow MM' \bot C'D'\)
Vậy \(\widehat {MM'O'}\) là góc phẳng nhị diện giữa mặt bên và đáy nhỏ, \(\widehat {M'MO}\) là góc phẳng nhị diện giữa mặt bên và đáy lớn.
Kẻ \(M'H \bot OM\left( {H \in OM} \right)\)
\(OMM'O'\) là hình chữ nhật
\( \Rightarrow OH = O'M' = \frac{a}{2},OM = a,MH = OM - OH = \frac{{\rm{a}}}{2}\)
\(\begin{array}{l}\tan \widehat {M'MO} = \frac{{M'H}}{{MH}} = 4\\ \Rightarrow \widehat {M'MO} = 75,{96^ \circ } \Rightarrow \widehat {MM'O'} = {180^ \circ } - \widehat {M'MO} = 104,{04^ \circ }\end{array}\)
b) Diện tích đáy lớn là: \(S = A{B^2} = 4{{\rm{a}}^2}\)
Diện tích đáy bé là: \(S' = A'B{'^2} = {a^2}\)
Thể tích hình chóp cụt là: \({V_1} = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.2a\left( {4{{\rm{a}}^2} + \sqrt {4{{\rm{a}}^2}.{a^2}} + {a^2}} \right) = \frac{{14{{\rm{a}}^3}}}{3}\)
Thể tích hình trụ rỗng là: \({V_2} = \pi {R^2}h = \pi .{\left( {\frac{a}{2}} \right)^2}.2{\rm{a}} = \frac{{\pi {a^3}}}{2}\)
Thể tích chân cột là: \(V = {V_1} - {V_2} = \left( {\frac{{14}}{3} - \frac{\pi }{2}} \right){a^3}\).
Bài 12 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình ôn tập chương 3. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Bài tập này thường bao gồm các dạng câu hỏi sau:
Để giúp học sinh giải bài tập này một cách dễ dàng, chúng tôi cung cấp hướng dẫn giải chi tiết cho từng câu hỏi. Hướng dẫn giải bao gồm các bước thực hiện, các công thức sử dụng và các lưu ý quan trọng.
Ví dụ:
Câu a: Giải phương trình sin(x) = 1/2
Giải:
Phương trình sin(x) = 1/2 có các nghiệm là:
Trong đó k là số nguyên.
Ngoài Bài 12 trang 87, chương 3 còn có nhiều bài tập tương tự. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để nắm vững kiến thức về hàm số lượng giác và phương trình lượng giác, học sinh nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Việc luyện tập thường xuyên sẽ giúp học sinh hiểu sâu hơn về các khái niệm và rèn luyện kỹ năng giải bài tập.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải Bài 12 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.