Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở đây, chúng tôi cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 1 - Chân trời sáng tạo, đặc biệt là mục 1 trang 7, 8, 9.
Mục tiêu của chúng tôi là giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong môn Toán.
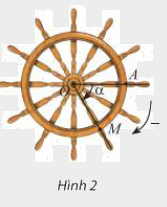
Hoạt động 1: Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA. a) Khi quay bánh lái ngược chiều kim đồng hồ ( Hình 1), cứ mỗi giây,
Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA.
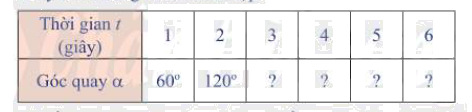
a) Khi quay bánh lái ngược chiều kim đồng hồ ( Hình 1), cứ mỗi giây, bánh lái quay một góc \( {60^0}\). Bảng dưới đây cho ta góc quay \(\alpha \)của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hơp.
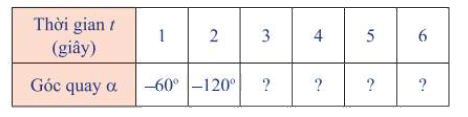
b) Nếu bánh lái được quay theo chiều ngược lại, nghĩa là quay cùng chiều kim đồng hồ ( Hình 2) với cùng tốc độ như trên, người ta ghi -\({60^ \circ }\)để chỉ góc mà thanh OM quay được sau mỗi giây. Bảng dưới đây cho ta góc quay \(\alpha \)của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hợp.
Phương pháp giải:
Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.
Lời giải chi tiết:
a)
Thời gian t (giây) | 1 | 2 | 3 | 4 | 5 | 6 |
Góc quay \(\alpha \) | \({60^ \circ }\) | \({120^ \circ }\) | \({180^ \circ }\) | \({240^ \circ }\) | \({300^ \circ }\) | \({360^ \circ }\) |
b)
Thời gian t (giây) | 1 | 2 | 3 | 4 | 5 | 6 |
Góc quay \(\alpha \) | -\({60^ \circ }\) | -\({120^ \circ }\) | -\({180^ \circ }\) | -\({240^ \circ }\) | -\({300^ \circ }\) | -\({360^ \circ }\) |
Cho \(\widehat {MON} = {60^ \circ }\). Xác định số đo của các góc lượng giác được biểu diễn trong Hình 6 và viết công thức tổng quát của số đo góc lượng giác (OM,ON).

Phương pháp giải:
- Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.
- Số đo của các góc lượng giác có cùng tia đầu Oa, và tia cuối Ob sai khác nhau một bội nguyên của \({360^ \circ }\)nên có công thức tổng quát là: \((Oa,Ob) = {\alpha ^ \circ } + k{360^ \circ }(k \in \mathbb{Z}),\)với \({\alpha ^ \circ }\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
Lời giải chi tiết:
a) Số đo của góc lượng giác (OM,ON) trong Hình 6 là \({60^ \circ }\)
b) Số đo của góc lượng giác (OM,ON) trong Hình 6 là \({60^ \circ } + {2.360^ \circ } = {780^ \circ }\)
c) Số đo của góc lượng giác (OM,ON) trong Hình 6 là \(\frac{5}{6}.( - {360^ \circ }) = - {300^ \circ }\)
Công thức tổng quát của số đo góc lượng giác \((OM,ON) = {60^ \circ } + k{360^ \circ }(k \in \mathbb{Z})\)
Trong khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là bao nhiêu độ?
Phương pháp giải:
- Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.
Lời giải chi tiết:
Đổi 2 giờ 15 phút = \(\frac{9}{4}\)giờ.
Trong khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là \(\frac{9}{4}.( - {360^ \circ }) = - {810^ \circ }\)
Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob), (Ob,Oc) và (Oa,Oc).
b) Nhận xét về mối liên hệ giữa ba số đo góc này.

Phương pháp giải:
- Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.
Lời giải chi tiết:
a) Số đo của góc lượng giác (Oa,Ob) trong Hình 7 là \({135^ \circ } + n{.360^ \circ },(n \in \mathbb{Z})\)
Số đo của góc lượng giác (Ob,Oc) trong Hình 7 là \( - {80^ \circ } + m{.360^ \circ },(m \in \mathbb{Z})\)
Số đo của góc lượng giác (Oa,Oc) trong Hình 7 là \({415^ \circ } + k{.360^ \circ },(k \in \mathbb{Z})\)
b)
\(\begin{array}{l}(Oa,Ob) + (Ob,Oc) = {135^ \circ } + n{.360^ \circ } + ( - {80^ \circ }) + m{.360^ \circ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {55^ \circ } + (n + m){.360^ \circ } = {415^ \circ } + (n + m - 1){.360^ \circ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {415^ \circ } + k{.360^ \circ } = (Oa,Oc)\end{array}\)
với \(k = n + m - 1\,;n,m,k \in \mathbb{Z}\)
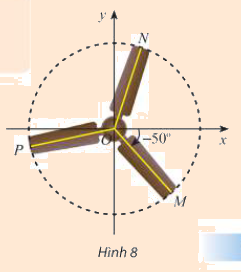
Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox,ON) và (Ox,OP).

Phương pháp giải:
- Số đo của các góc lượng giác có cùng tia đầu Oa, và tia cuối Ob sai khác nhau một bội nguyên của \({360^ \circ }\)nên có công thức tổng quát là: \((Oa,Ob) = {\alpha ^ \circ } + k{360^ \circ }(k \in \mathbb{Z}),\)với \({\alpha ^ \circ }\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
- Quy ước chiều quay ngược chiều kim đồng hồ là chiều dương và chiều quay cùng chiều kim đồng hồ là chiều âm.
Lời giải chi tiết:
Công thức tổng quát số đo của góc lượng giác \((Ox,ON) = {70^ \circ } + k{360^ \circ }(k \in \mathbb{Z})\)
Công thức tổng quát số đo của góc lượng giác \((Ox,OP) = (Ox,OM) + (OM,OP) = - {50^ \circ } + ( - {120^ \circ }) + m{360^ \circ } = - {170^ \circ } + m{360^ \circ }\,\,\,\,,(m \in \mathbb{Z})\)
Mục 1 của SGK Toán 11 tập 1 - Chân trời sáng tạo tập trung vào việc giới thiệu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng trong chương trình Toán học, mở đầu cho các kiến thức về đạo hàm và tích phân. Việc hiểu rõ về giới hạn hàm số sẽ giúp học sinh tiếp cận các khái niệm nâng cao một cách dễ dàng hơn.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1, trang 7, 8, 9 của SGK Toán 11 tập 1 - Chân trời sáng tạo:
a) lim (x→2) (x^2 + 3x - 1)
Lời giải: Áp dụng tính chất giới hạn của hàm đa thức, ta có:
lim (x→2) (x^2 + 3x - 1) = 2^2 + 3*2 - 1 = 4 + 6 - 1 = 9
b) lim (x→-1) (x^3 - 2x + 5)
Lời giải: Tương tự như trên, ta có:
lim (x→-1) (x^3 - 2x + 5) = (-1)^3 - 2*(-1) + 5 = -1 + 2 + 5 = 6
a) lim (x→3) (2x + 1)/(x - 1)
Lời giải: Áp dụng tính chất giới hạn của hàm phân thức, ta có:
lim (x→3) (2x + 1)/(x - 1) = (2*3 + 1)/(3 - 1) = 7/2
b) lim (x→0) (x^2 + 1)/(x + 2)
Lời giải: Tương tự như trên, ta có:
lim (x→0) (x^2 + 1)/(x + 2) = (0^2 + 1)/(0 + 2) = 1/2
a) lim (x→1) (x^2 - 1)/(x - 1)
Lời giải: Ta có thể phân tích tử thức thành (x - 1)(x + 1). Do đó:
lim (x→1) (x^2 - 1)/(x - 1) = lim (x→1) (x + 1) = 1 + 1 = 2
b) lim (x→2) (x^3 - 8)/(x - 2)
Lời giải: Ta có thể phân tích tử thức thành (x - 2)(x^2 + 2x + 4). Do đó:
lim (x→2) (x^3 - 8)/(x - 2) = lim (x→2) (x^2 + 2x + 4) = 2^2 + 2*2 + 4 = 4 + 4 + 4 = 12
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về nội dung của mục 1 và tự tin giải các bài tập trong SGK Toán 11 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!