Bài 11 trang 128 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến phép biến hình. Bài tập này giúp học sinh củng cố kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 11 trang 128, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
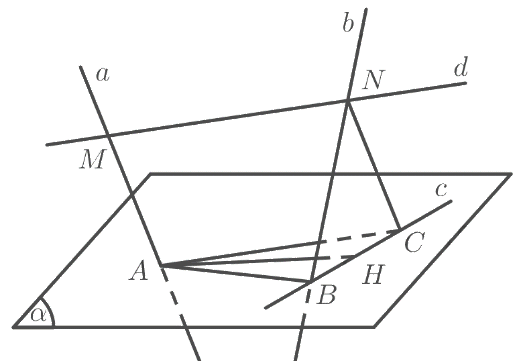
Cho mặt phẳng \(\left( \alpha \right)\) và hai đường thẳng chéo nhau \(a,b\) cắt \(\left( \alpha \right)\) tại \(A\) và \(B\). Gọi \(d\) là đường thẳng thay đổi luôn luôn song song với \(\left( \alpha \right)\) và cắt \(a\) tại \(M\), cắt \(b\) tại \(N\). Qua điểm \(N\) dựng đường thẳng song song với \(a\) cắt \(\left( \alpha \right)\) tại điểm \(C\).
Đề bài
Cho mặt phẳng \(\left( \alpha \right)\) và hai đường thẳng chéo nhau \(a,b\) cắt \(\left( \alpha \right)\) tại \(A\) và \(B\). Gọi \(d\) là đường thẳng thay đổi luôn luôn song song với \(\left( \alpha \right)\) và cắt \(a\) tại \(M\), cắt \(b\) tại \(N\). Qua điểm \(N\) dựng đường thẳng song song với \(a\) cắt \(\left( \alpha \right)\) tại điểm \(C\).
a) Tứ giác \(MNCA\) là hình gì?
b) Chứng minh rằng điểm \(C\) luôn luôn chạy trên một đường thẳng cố định.
c) Xác định vị trí của đường thẳng \(d\) để độ dài \(MN\) nhỏ nhất.
Phương pháp giải - Xem chi tiết
Sử dụng hệ quả: Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Lời giải chi tiết
a) Ta có:
\(\left. \begin{array}{l}d \subset \left( {AMNC} \right)\\d\parallel \left( \alpha \right)\\\left( \alpha \right) \cap \left( {AMNC} \right) = AC\end{array} \right\} \Rightarrow d\parallel AC \Rightarrow MN\parallel AC\)
Mà \(a\parallel NC \Rightarrow MA\parallel NC\)
\( \Rightarrow AMNC\) là hình bình hành.
b) Gọi \(\left( \beta \right)\) là mặt phẳng chứa \(b\) và song song với \(a\), \(c = \left( \alpha \right) \cap \left( \beta \right)\)
Ta có:
\(\left. \begin{array}{l}NC\parallel a\\N \in b\end{array} \right\} \Rightarrow NC \subset \left( \beta \right)\)
\( \Rightarrow C \in \left( \alpha \right) \cap \left( \beta \right) \Rightarrow C \in c\)
Vậy điểm \(C\) luôn luôn chạy trên đường thẳng \(c\) là giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) cố định.
c) Trong mặt phẳng \(\left( \alpha \right)\), kẻ \(AH \bot c\)
Vì \(c\) cố định nên \(AC \ge AH\)
\(AMNC\) là hình bình hành \( \Rightarrow MN = AC\)
Vậy \(MN \ge AH\)
Vậy \(MN\) nhỏ nhất khi \(C \equiv H\). Khi đó \(d\parallel AH\).
Bài 11 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh ôn luyện và củng cố kiến thức về các phép biến hình. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 11 yêu cầu học sinh thực hiện các phép biến hình (tịnh tiến, quay, đối xứng trục, đối xứng tâm) lên các hình cho trước. Để giải bài tập này, học sinh cần nắm vững định nghĩa, tính chất và cách thực hiện của từng phép biến hình.
Để giải bài tập này, ta cần xác định các yếu tố quan trọng của phép biến hình, như tâm quay, góc quay, vectơ tịnh tiến, trục đối xứng, tâm đối xứng. Sau đó, áp dụng công thức biến hình để tìm ra ảnh của các điểm và hình đã cho.
Ví dụ, xét phép tịnh tiến theo vectơ v = (a; b). Ảnh của điểm M(x; y) qua phép tịnh tiến này là điểm M'(x + a; y + b).
Tương tự, xét phép quay tâm O góc α. Ảnh của điểm M(x; y) qua phép quay này là điểm M'(x'; y') thỏa mãn:
Ngoài bài 11 trang 128, còn rất nhiều bài tập tương tự về các phép biến hình trong SGK Toán 11 tập 1 - Chân trời sáng tạo. Học sinh nên luyện tập thêm các bài tập này để nắm vững kiến thức và kỹ năng giải bài tập.
Các phép biến hình có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Khi giải bài tập về phép biến hình, học sinh cần lưu ý:
Bài 11 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép biến hình. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để tìm hiểu thêm về các bài giải Toán 11 và các môn học khác.