Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 37, 38, 39 sách giáo khoa Toán 11 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Quãng đường rơi tự do của một vật được biểu diễn bởi công thức
Quãng đường rơi tự do của một vật được biểu diễn bởi công thức \(s\left( t \right) = 4,9{t^2}\) với \(t\) là thời gian tính bằng giây và \(s\) tính bằng mét.
Vận tốc trung bình của chuyển động này trên khoảng thời gian \(\left[ {5;t} \right]\) hoặc \(\left[ {t;5} \right]\) được tính bằng công thức \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\).
a) Hoàn thiện bảng sau về vận tốc trung bình trong những khoảng thời gian khác nhau. Nêu nhận xét về \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\) khi \(t\) càng gần 5.

b) Giới hạn \(\mathop {\lim }\limits_{t \to 5} \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\) được gọi là vận tốc tức thời của chuyển động tại thời điểm \({t_0} = 5\). Tính giá trị này.
c) Tính giới hạn \(\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}}\) để xác định vận tốc tức thời của chuyển động tại thời điểm \({t_0}\) nào đó trong quá trình rơi của vật.
Phương pháp giải:
a) Thay vào công thức \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\).
b) c) Sử dụng các quy tắc tính giới hạn.
Lời giải chi tiết:
a)
\(\begin{array}{l}\begin{array}{*{20}{l}}{\left[ {5;5,1} \right]}\end{array}:t = 5,1 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{1^2} - 4,{{9.5}^2}}}{{5,1 - 5}} = 49,49\\\begin{array}{*{20}{l}}{\left[ {5;5,05} \right]}\end{array}:t = 5,05 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{05}^2} - 4,{{9.5}^2}}}{{5,05 - 5}} = 49,245\\\begin{array}{*{20}{l}}{\left[ {5;5,01} \right]}\end{array}:t = 5,01 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{01}^2} - 4,{{9.5}^2}}}{{5,01 - 5}} = 49,049\\\begin{array}{*{20}{l}}{\left[ {5;5,001} \right]}\end{array}:t = 5,001 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.5,{{001}^2} - 4,{{9.5}^2}}}{{5,001 - 5}} = 49,0049\\\begin{array}{*{20}{l}}{\left[ {4,999;5} \right]}\end{array}:t = 4,999 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{999}^2} - 4,{{9.5}^2}}}{{4,999 - 5}} = 48,9951\\\begin{array}{*{20}{l}}{\left[ {4,99;5} \right]}\end{array}:t = 4,99 \Rightarrow \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \frac{{4,9.4,{{99}^2} - 4,{{9.5}^2}}}{{4,99 - 5}} = 48,951\end{array}\)
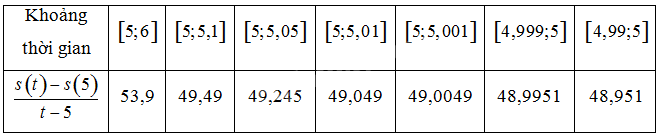
Ta thấy: \(\frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}}\) càng gần 49 khi \(t\) càng gần 5.
b)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to 5} \frac{{s\left( t \right) - s\left( 5 \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,{{9.5}^2}}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - {5^2}} \right)}}{{t - 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - 5} \right)\left( {t + 5} \right)}}{{t - 5}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + 5} \right) = 4,9\left( {5 + 5} \right) = 49\end{array}\)
c)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9{t^2} - 4,9.t_0^2}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {{t^2} - t_0^2} \right)}}{{t - t_0^2}} = \mathop {\lim }\limits_{t \to 5} \frac{{4,9\left( {t - {t_0}} \right)\left( {t + {t_0}} \right)}}{{t - {t_0}}}\\ = \mathop {\lim }\limits_{t \to 5} 4,9\left( {t + {t_0}} \right) = 4,9\left( {{t_0} + {t_0}} \right) = 9,8{t_0}\end{array}\)
Tính đạo hàm của hảm số \(f\left( x \right) = {x^3}\).
Phương pháp giải:
Tính giới hạn \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\).
Lời giải chi tiết:
Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(\begin{array}{l}f\prime ({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - {x_0}^3}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x.{x_0} + {x_0}^2} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x.{x_0} + {x_0}^2} \right) = {x^2} + {x_0}.{x_0} + {x_0}^2 = 3{x_0}^2\end{array}\)
Vậy \(f'\left( x \right) = {\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}\) trên \(\mathbb{R}\).
Với tình huống trong Hoạt động mở đầu, hãy tính vận tốc tức thời của chuyển động lúc \(t = 2\).
Phương pháp giải:
Tính \(v\left( 2 \right) = s'\left( 2 \right)\) với \(s\left( t \right) = 4,9{t^2}\).
Lời giải chi tiết:
Với bất kì \({t_0} \in \mathbb{R}\), ta có:
\(s'\left( {{t_0}} \right) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}} = 9,8{t_0}\)
Vậy \(s'\left( t \right) = 9,8t\) trên \(\mathbb{R}\).
Vậy vận tốc tức thời của chuyển động lúc \(t = 2\) là: \(v\left( 2 \right) = s'\left( 2 \right) = 9,8.2 = 19,6\left( {m/s} \right)\)
Mục 1 của chương trình Toán 11 tập 2 - Chân trời sáng tạo tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng, nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập trong mục này là vô cùng cần thiết.
Để giải tốt các bài tập trong Mục 1, các em cần:
a) f(x) = x3 - 2x2 + 5x - 1
Giải: f'(x) = 3x2 - 4x + 5
b) g(x) = (x2 + 1)(x - 2)
Giải: g'(x) = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Giải: y' = cos(2x + 1) * 2 = 2cos(2x + 1)
Giải:
f(1) = 12 + 3(1) - 2 = 2
f'(x) = 2x + 3
f'(1) = 2(1) + 3 = 5
Phương trình tiếp tuyến: y - 2 = 5(x - 1) => y = 5x - 3
Trong quá trình giải bài tập về đạo hàm, các em cần chú ý:
Hy vọng với những hướng dẫn chi tiết và lời giải cụ thể trên đây, các em sẽ tự tin hơn trong việc giải các bài tập về đạo hàm. Chúc các em học tập tốt!