Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4, trang 78, 79, 80, 81 sách giáo khoa Toán 11 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho một khối hộp chữ nhật với các kích thước là (a,b,c)
Cho một khối hộp chữ nhật với các kích thước là \(a,b,c\) đều là số nguyên dương. Về các mặt phẳng song song với các mặt của hình hộp và chia nó thành các khối lập phương có cạnh bằng 1 (Hình 11). Tìm số hình lập phương đơn vị có trong hình hộp.
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
Số hình lập phương đơn vị có trong hình hộp là: \(abc\).
Cho khối lăng trụ tam giác \(ABC.A'B'C'\) (Hình 14). Tìm cách chia khối lăng trụ thành ba khối chóp có cùng chiều cao và diện tích đáy.

Phương pháp giải:
Chia khối lăng trụ thành ba khối chóp có đáy là một trong hai đáy của lăng trụ, đỉnh nằm trên đáy còn lại.
Lời giải chi tiết:
Chia khối lăng trụ tam giác \(ABC.A'B'C'\) thành ba khối chóp: \(A.A'B'C',B'.ABC\) và \(C.A'B'C'\).
Tính thể tích của một bồn chứa có dạng khối chóp cụt đều có kích thước được cho như trong Hình 20.

Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).
Lời giải chi tiết:
Diện tích đáy lớn là: \(S = {5^2} = 25\left( {{m^2}} \right)\)
Diện tích đáy bé là: \(S' = {2^2} = 4\left( {{m^2}} \right)\)
Thể tích của bồn chứa là: \(V = \frac{1}{3}.3\left( {25 + \sqrt {25.4} + 4} \right) = 39\left( {{m^3}} \right)\)
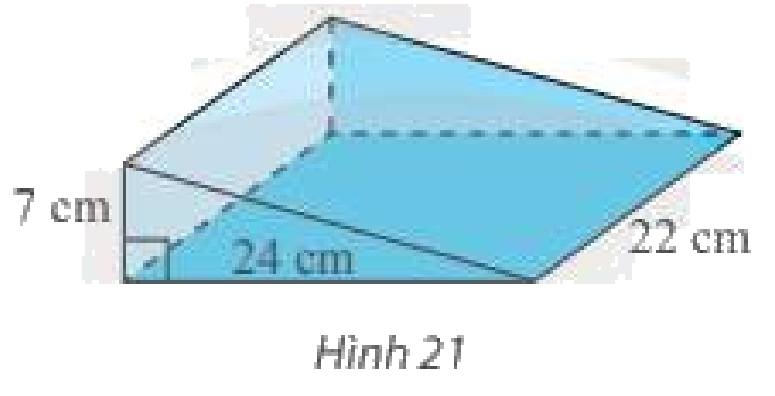
Tính thể tích cái nêm hình lăng trụ đứng có kích thước như trong Hình 21.

Phương pháp giải:
Sử dụng công thức tính thể tích khối lăng trụ: \(V = Sh\).
Lời giải chi tiết:
Diện tích đáy của lăng trụ là: \(\frac{1}{2}.7.24 = 84\left( {c{m^2}} \right)\)
Thể tích cái nêm hình lăng trụ đứng là: \(84.22 = 1848\left( {c{m^3}} \right)\)
Mục 4 của SGK Toán 11 tập 2 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Dưới đây là hướng dẫn chi tiết và lời giải cho từng bài tập trang 78, 79, 80, 81.
Các bài tập trang 78 thường là những bài tập áp dụng trực tiếp các kiến thức đã học. Ví dụ, có thể là bài tập về tính đạo hàm của hàm số, tìm cực trị của hàm số, hoặc khảo sát hàm số. Để giải các bài tập này, học sinh cần:
Trang 79 có thể chứa các bài tập nâng cao hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học và kết hợp với các kỹ năng giải toán khác. Ví dụ, có thể là bài tập về ứng dụng đạo hàm để giải quyết các bài toán thực tế. Để giải các bài tập này, học sinh cần:
Các bài tập trang 80 và 81 thường là các bài tập tổng hợp, đòi hỏi học sinh phải nắm vững kiến thức của cả mục 4. Ví dụ, có thể là bài tập về vẽ đồ thị hàm số, tìm điểm uốn của hàm số, hoặc giải phương trình chứa đạo hàm. Để giải các bài tập này, học sinh cần:
Cho hàm số y = x3 - 3x2 + 2. Tìm đạo hàm của hàm số.
Lời giải:
y' = 3x2 - 6x
Trong quá trình giải bài tập, học sinh cần lưu ý một số điều sau:
Hy vọng với hướng dẫn chi tiết và lời giải cụ thể này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 11 tập 2 Chân trời sáng tạo. Chúc các em học tập tốt!
| Chủ đề | Nội dung |
|---|---|
| Đạo hàm | Công thức, tính chất, ứng dụng |
| Cực trị hàm số | Tìm cực đại, cực tiểu |
| Khảo sát hàm số | Vẽ đồ thị, tìm điểm uốn |
Ngoài ra, các em có thể tham khảo thêm các bài giảng trực tuyến, video hướng dẫn và các tài liệu học tập khác để nâng cao kiến thức và kỹ năng giải toán.