Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 37, 38 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập trong mục này tập trung vào các kiến thức quan trọng của chương trình, đòi hỏi các em phải vận dụng linh hoạt các công thức và định lý đã học.
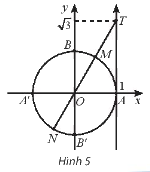
Trong mặt phẳng toạ độ Oxy, cho T là điểm trên trục tang có toạ độ là (left( {1;sqrt 3 } right)) (Hình 5).
Trong mặt phẳng toạ độ Oxy, cho T là điểm trên trục tang có toạ độ là \(\left( {1;\sqrt 3 } \right)\) (Hình 5). Những điểm nào trên đường tròn lượng giác x có \(tanx = \sqrt 3 \)? Xác định số đo của các góc lượng giác đó.
Phương pháp giải:
Quan sát hình vẽ để trả lời.
Lời giải chi tiết:
Những điểm biểu diễn góc x trên đường tròn lượng giác có \(tanx = \sqrt 3 \) là M và N.
Điểm M là điểm biểu diễn các góc lượng giác có số đo \(\frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\).
Điểm N là điểm biểu diễn các góc lượng giác có số đo \( - \frac{{2\pi }}{3} + k\pi ,k \in \mathbb{Z}\).
Giải các phương trình sau:
\(\begin{array}{*{20}{l}}{a){\rm{ }}tanx = 0;}\\{b){\rm{ }}tan\left( {30^\circ --3x} \right) = tan75^\circ .}\end{array}\)
Phương pháp giải:
Với mọi \(m \in \mathbb{R}\), tồn tại duy nhất \(\alpha \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) thoả mãn \(\tan \alpha = m\). Khi đó:
\(\tan {\rm{x}} = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb{Z}.\)
\(\tan x = \tan {\alpha ^o} \Leftrightarrow x = {\alpha ^o} + k{180^o},k \in \mathbb{Z}.\)
Lời giải chi tiết:
a) Điều kiện xác định là: \(x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
Vì tan0 = 0 nên phương trình tanx = 0 có các nghiệm \(x = k\pi ,{\rm{ }}k\; \in \;\mathbb{Z}.\)
Vậy tập nghiệm của phương trình là: \(S = \{ k\pi ,{\rm{ }}k\; \in \;\mathbb{Z}\} .\)
\(\begin{array}{*{20}{l}}{b){\rm{ }}tan\left( {30^\circ -3x} \right) = tan75^\circ }\\{ \Leftrightarrow \;tan\left( {3x-30^\circ } \right) = tan\left( {-{\rm{ }}75^\circ } \right)}\\{ \Leftrightarrow \;3x-30^\circ = -75^\circ + k180^\circ ,k\; \in \;\mathbb{Z}}\\{ \Leftrightarrow \;3x = -\,45^\circ + k180^\circ ,k\; \in \;\mathbb{Z}}\\{ \Leftrightarrow \;x = -15^\circ + k60^\circ ,k\; \in \;\mathbb{Z}.}\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \{ -15^\circ + k60^\circ ,{\rm{ }}k\; \in \;\mathbb{Z}\} .\)
\(\begin{array}{l}{\rm{c) cos}}\left( {x + \frac{\pi }{{12}}} \right) = {\rm{cos}}\frac{{3\pi }}{{12}}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{{12}} = \frac{{3\pi }}{{12}} + k2\pi \\x + \frac{\pi }{{12}} = - \frac{{3\pi }}{{12}} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {\frac{\pi }{6} + k2\pi ; - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}} \right\}\)
Mục 4 của SGK Toán 11 tập 1 chương trình Chân trời sáng tạo thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo, đặc biệt là trong hình học không gian.
Phép tịnh tiến là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ. Để thực hiện một phép tịnh tiến, ta cần xác định vectơ tịnh tiến. Vectơ tịnh tiến này sẽ chỉ ra hướng và độ dài của sự dịch chuyển.
Phép quay là phép biến hình biến mỗi điểm M thành điểm M’ sao cho khoảng cách từ M đến tâm quay O bằng khoảng cách từ M’ đến tâm quay O và góc giữa OM và OM’ bằng một góc α cho trước.
Phép đối xứng trục là phép biến hình biến mỗi điểm M thành điểm M’ sao cho đường thẳng nối M và M’ vuông góc với trục đối xứng và trung điểm của đoạn MM’ nằm trên trục đối xứng.
Phép đối xứng tâm là phép biến hình biến mỗi điểm M thành điểm M’ sao cho M là trung điểm của đoạn MM’.
Để giải các bài tập trong mục 4 trang 37, 38 SGK Toán 11 tập 1, các em cần:
Ví dụ, bài tập yêu cầu tìm ảnh của điểm A(1; 2) qua phép tịnh tiến theo vectơ v = (3; -1). Ta áp dụng công thức M’(x0 + a; y0 + b) để tìm A’(1 + 3; 2 - 1) = A’(4; 1).
Để nắm vững kiến thức về các phép biến hình, các em nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Việc giải nhiều bài tập sẽ giúp các em hiểu rõ hơn về bản chất của các phép biến hình và rèn luyện kỹ năng giải bài tập.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em sẽ tự tin hơn trong việc học tập môn Toán 11. Chúc các em học tốt!