Chào mừng bạn đến với bài học về lý thuyết Hàm số liên tục trong chương trình Toán 11 Chân trời sáng tạo tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và quan trọng nhất về hàm số liên tục, giúp bạn giải quyết các bài tập một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, điều kiện liên tục của hàm số, các tính chất và ứng dụng của hàm số liên tục trong thực tế.
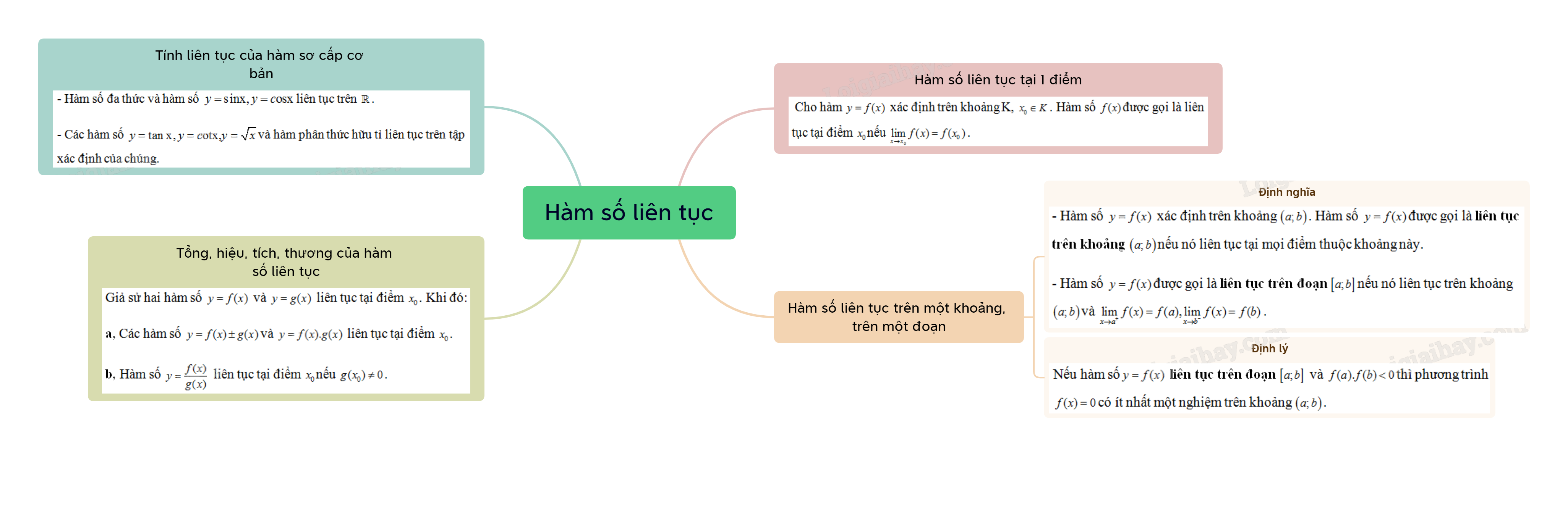
1. Hàm số liên tục tại 1 điểm
1. Hàm số liên tục tại 1 điểm
Cho hàm \(y = f(x)\) xác định trên khoảng K, \({x_0} \in K\). Hàm số \(f(x)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\).
Hàm số không liên tục tại \({x_0}\) được gọi là gián đoạn tại điểm đó.
*Nhận xét: Để hàm số \(y = f(x)\) liên tục tại \({x_0}\) thì phải có cả 3 điều sau:
2. Hàm số liên tục trên một khoảng, trên một đoạn
- Hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;b} \right)\)
Hàm số \(y = f(x)\)được gọi là liên tục trên khoảng \(\left( {a;b} \right)\)nếu nó liên tục tại mọi điểm thuộc khoảng này.
- Hàm số \(y = f(x)\)được gọi là liên tục trên đoạn \(\left[ {a;b} \right]\)nếu nó liên tục trên khoảng \(\left( {a;b} \right)\)và \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a),\mathop {\lim }\limits_{x \to {b^ - }} f(x) = f(b)\).
* Nhận xét:
- Đồ thị hàm số liên tục trên một khoảng, đoạn là “đường liền” trên khoảng, đoạn đó.
- Nếu hàm số\(y = f(x)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và \(f(a).f(b) < 0\)thì phương trình \(f(x) = 0\)có ít nhất một nghiệm trên khoảng \(\left( {a;b} \right)\).
3. Tính liên tục của hàm sơ cấp cơ bản
- Hàm số đa thức và hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}},y = c{\rm{osx}}\) liên tục trên \(\mathbb{R}\).
- Các hàm số \(y = \tan {\rm{x}},y = c{\rm{otx,}}y = \sqrt x \)và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác định của chúng.
2. Tổng, hiệu, tích, thương của hàm số liên tục
Giả sử hai hàm số \(y = f(x)\) và \(y = g(x)\) liên tục tại điểm \({x_0}\). Khi đó:
a, Các hàm số \(y = f(x) \pm g(x)\)và \(y = f(x).g(x)\) liên tục tại điểm \({x_0}\).
b, Hàm số \(y = \frac{{f(x)}}{{g(x)}}\) liên tục tại điểm \({x_0}\)nếu \(g({x_0}) \ne 0\).
Hàm số liên tục là một khái niệm cơ bản và quan trọng trong giải tích, đóng vai trò nền tảng cho nhiều kiến thức nâng cao hơn. Trong chương trình Toán 11 Chân trời sáng tạo, việc nắm vững lý thuyết hàm số liên tục là điều kiện cần thiết để giải quyết các bài toán liên quan đến giới hạn, đạo hàm và tích phân.
Hàm số f(x) được gọi là liên tục tại điểm x0 nếu thỏa mãn ba điều kiện sau:
Nói cách khác, một hàm số liên tục tại một điểm nếu đồ thị của nó không bị đứt gãy tại điểm đó.
Hàm số f(x) được gọi là liên tục trên khoảng (a; b) nếu nó liên tục tại mọi điểm thuộc khoảng đó.
Các hàm số liên tục có một số tính chất quan trọng sau:
Nếu f(x) là hàm đa thức, hàm hữu tỉ (phân thức) trên miền xác định của nó, hoặc hàm lượng giác thì f(x) liên tục trên miền xác định của nó.
Lý thuyết hàm số liên tục có nhiều ứng dụng trong thực tế, ví dụ:
Ví dụ 1: Xét hàm số f(x) = x2 + 1. Hàm số này là hàm đa thức nên liên tục trên R.
Ví dụ 2: Xét hàm số f(x) = 1/x. Hàm số này là hàm hữu tỉ và liên tục trên khoảng (−∞; 0) và (0; +∞).
Lý thuyết hàm số liên tục là nền tảng cho việc học về giới hạn, đạo hàm và tích phân. Việc hiểu rõ khái niệm hàm số liên tục sẽ giúp bạn dễ dàng tiếp thu các kiến thức nâng cao hơn trong giải tích.
Để nắm vững lý thuyết hàm số liên tục, bạn nên luyện tập giải nhiều bài tập khác nhau. Hãy tìm các bài tập trong SGK Toán 11 Chân trời sáng tạo và các tài liệu tham khảo khác để rèn luyện kỹ năng của mình.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết Hàm số liên tục - SGK Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!