Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo

Chào mừng bạn đến với bài học về lý thuyết Hàm số mũ và Hàm số lôgarit trong chương trình Toán 11 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng quan trọng, giúp bạn hiểu rõ về hai loại hàm số đặc biệt này.

Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, đồ thị và các ứng dụng thực tế của hàm số mũ và hàm số lôgarit.

1. Hàm số mũ - Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.

1. Hàm số mũ

- Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.

- Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có:

+ Tập xác định: \(D = \mathbb{R}\).

+ Tập giá trị: \(T = \left( {0; + \infty } \right)\).

+ Hàm số liên tục trên \(\mathbb{R}\).

+ Sự biến thiên:

Nếu a > 1 thì hàm số đồng biến trên \(\mathbb{R}\) và \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = 0\).
Nếu 0 < a < 1 thì hàm số nghịch biến trên \(\mathbb{R}\) và \(\mathop {\lim }\limits_{x \to + \infty } y = 0;\mathop {\lim }\limits_{x \to - \infty } y = + \infty \).

+ Đồ thị:

Cắt trục tung tại điểm (0; 1), đi qua điểm (1; a).
Nằm phía trên trục hoành.

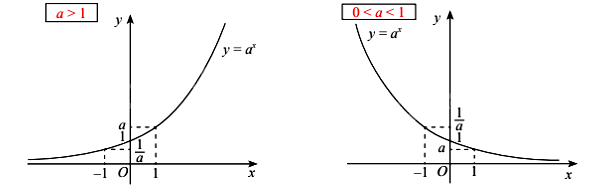
Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo 1

2. Hàm số lôgarit

- Hàm số \(y = {\log _a}x\left( {a > 0;a \ne 1} \right)\) được gọi là hàm số lôgarit cơ số a.

- Hàm số \(y = {\log _a}x\left( {a > 0;a \ne 1} \right)\) có:

+ Tập xác định: \(D = \left( {0; + \infty } \right)\).

+ Tập giá trị: \(T = \mathbb{R}\).

+ Hàm số liên tục trên \(\left( {0; + \infty } \right)\).

+ Sự biến thiên:

Nếu a > 1 thì hàm số đồng biến trên \(\left( {0; + \infty } \right)\) và \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to {0^ + }} y = 0\).
Nếu 0 < a < 1 thì hàm số nghịch biến trên \(\left( {0; + \infty } \right)\) và \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty \).

+ Đồ thị:

Cắt trục hoành tại điểm (1; 0), đi qua điểm (a; 1).
Nằm phía phải trục tung.

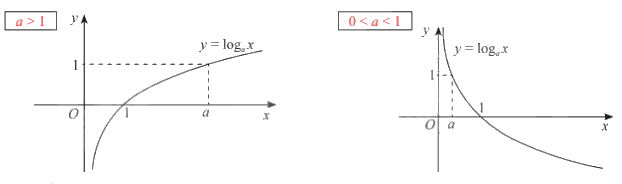
Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo 2

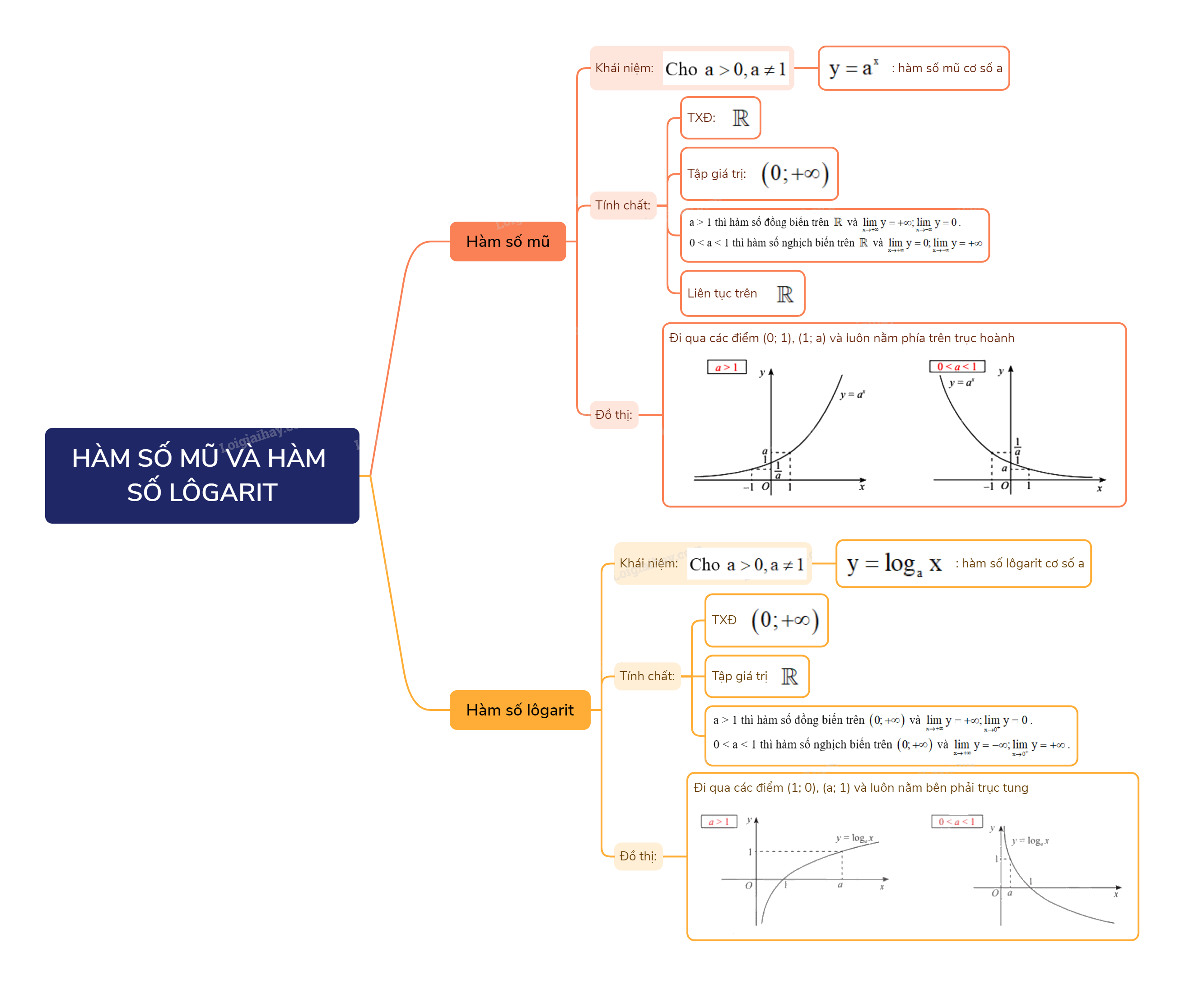
Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo 3

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo – hành trang không thể thiếu trong chuyên mục Giải bài tập Toán 11 trên nền tảng toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Lý thuyết Hàm số mũ. Hàm số lôgarit - Toán 11 Chân trời sáng tạo

Hàm số mũ và hàm số lôgarit là hai khái niệm quan trọng trong chương trình Toán 11, đặc biệt là trong chương trình Chân trời sáng tạo. Việc nắm vững lý thuyết và kỹ năng giải bài tập liên quan đến hai hàm số này là nền tảng để học tốt các kiến thức toán học nâng cao hơn.

I. Hàm số mũ

1. Định nghĩa: Hàm số mũ là hàm số có dạng y = a^x, trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1). x là biến số thực.

2. Tập xác định: Tập xác định của hàm số mũ y = a^x là tập số thực ℝ.

3. Tính chất:

Nếu a > 1: Hàm số mũ y = a^x là hàm số đồng biến trên ℝ.
Nếu 0 < a < 1: Hàm số mũ y = a^x là hàm số nghịch biến trên ℝ.
Hàm số mũ luôn dương với mọi x ∈ ℝ.

4. Đồ thị:

Đồ thị của hàm số mũ y = a^x có các đặc điểm sau:

Luôn đi qua điểm A(0, 1).
Có tiệm cận ngang là trục hoành (y = 0).

II. Hàm số lôgarit

1. Định nghĩa: Hàm số lôgarit là hàm số có dạng y = log_ax, trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1). x là biến số thực dương.

2. Tập xác định: Tập xác định của hàm số lôgarit y = log_ax là tập số thực dương (0, +∞).

3. Tính chất:

Nếu a > 1: Hàm số lôgarit y = log_ax là hàm số đồng biến trên (0, +∞).
Nếu 0 < a < 1: Hàm số lôgarit y = log_ax là hàm số nghịch biến trên (0, +∞).

4. Đồ thị:

Đồ thị của hàm số lôgarit y = log_ax có các đặc điểm sau:

Luôn đi qua điểm A(1, 0).
Có tiệm cận đứng là trục tung (x = 0).

III. Mối quan hệ giữa hàm số mũ và hàm số lôgarit

Hàm số mũ và hàm số lôgarit là hai hàm số nghịch đảo của nhau. Điều này có nghĩa là:

a^log_ax = x với mọi x > 0
log_aa^x = x với mọi x ∈ ℝ

IV. Bài tập ví dụ

Bài 1: Giải phương trình 2^x = 8

Giải: Ta có 2^x = 2³, suy ra x = 3.

Bài 2: Tính log₃9

Giải: Ta có log₃9 = log₃3² = 2.

V. Ứng dụng của hàm số mũ và hàm số lôgarit

Hàm số mũ và hàm số lôgarit có nhiều ứng dụng trong thực tế, bao gồm:

Trong tài chính: Tính lãi kép, tính giá trị tương lai của một khoản đầu tư.
Trong khoa học: Mô tả sự tăng trưởng dân số, sự phân rã phóng xạ.
Trong kỹ thuật: Tính toán tín hiệu, xử lý ảnh.

Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết Hàm số mũ và Hàm số lôgarit trong chương trình Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!