Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 17, 18, 19 sách Giáo khoa Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 11 và đạt kết quả cao trong học tập.
Cho (alpha = frac{pi }{3}). Biểu diễn các góc lượng giác ( - alpha ,alpha + pi ,pi - alpha ,frac{pi }{2} - alpha ) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc (alpha )
Cho \(\alpha = \frac{\pi }{3}\). Biểu diễn các góc lượng giác \( - \alpha ,\alpha + \pi ,\pi - \alpha ,\frac{\pi }{2} - \alpha \) trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc \(\alpha \)
Phương pháp giải:
Vẽ đường tròn lượng giác dựa vào kiến thức đã học rồi nhận xét
Lời giải chi tiết:
Dựa vào đường tròn lượng giác ta nhận được:
\(\left. \begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \end{array} \right\} \Rightarrow \left\{ \begin{array}{l}tan\left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array} \right.\)
\(\left. \begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array} \right.\)
\(\begin{array}{l}\left. \begin{array}{l}\sin \left( {\pi - \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\pi - \frac{\pi }{3}} \right) = - \frac{1}{2},\,\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\sin \left( {\pi - \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\\\cos \left( {\pi - \frac{\pi }{3}} \right) = - \cos \frac{\pi }{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
\(\begin{array}{l}\left. \begin{array}{l}\sin \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \frac{1}{2},\,\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\sin \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \cos \frac{\pi }{3}\\\cos \left( {\frac{\pi }{2} - \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array} \right.\end{array}\)
a) Biểu diễn \(\cos 638^\circ \) qua gí trị lượng giác của góc có số đo từ \(0^\circ \) đến \(45^\circ \)
b) Biểu diễn \(\cot \frac{{19\pi }}{5}\) qua giá trị lượng giác của góc có số đo từ 0 đến \(\frac{\pi }{4}\)
Phương pháp giải:
Dựa vào ví dụ 4 để làm bài
Lời giải chi tiết:
a) \(\cos 638^\circ = \cos \left( {4.180^\circ + 90^\circ - 8^\circ } \right) = - \cos \left( {90^\circ - 8^\circ } \right) = - \sin 8^\circ \)
b) \(\cot \left( {\frac{{19\pi }}{5}} \right) = \cot \left( {4\pi - \frac{\pi }{5}} \right) = - \cot \left( {\frac{\pi }{5}} \right)\)
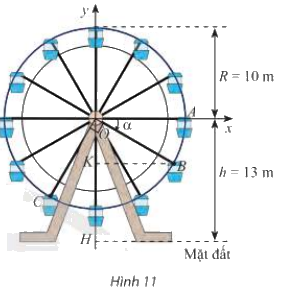
Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu với điểm B và C.

a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng \(\left( {13 + 10\sin \alpha } \right)\) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi \(\alpha = - 30^\circ \)
b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải:
Dựa vào kiến thức lượng giác đã học để tính.
Lời giải chi tiết:
a) Chiều cao từ điểm B đến mặt đất là độ dài đoạn KH.
Điểm B là điểm biểu diễn cho góc lượng giác có số đo góc là \(\alpha \) trên đường tròn lượng giác có bán kính bằng 10 nên tọa độ điểm \(B(10\cos \alpha ;10\sin \alpha )\).
Vì tung độ điểm B có giá trị âm nên \(10\sin \alpha < 0\), suy ra độ dài \(OH = \left| {10\sin \alpha } \right| = - 10\sin \alpha \).
Ta có \(KH = OH - OK = 13 - ( - 10\sin \alpha ) = 13 + 10\sin \alpha \) (mét).
Với \(\alpha = - 30^\circ \Rightarrow KH = 13 + 10.\sin \left( { - 30^\circ } \right) = 8\,\,\left( m \right)\).
b) Nếu B cách mặt đất 4m \( \Rightarrow 4 = 13 + 10\sin \alpha \Leftrightarrow \sin \alpha = - \frac{9}{{10}}\).
Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\left( { - \frac{9}{{10}}} \right)^2} + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = - \frac{{\sqrt {19} }}{{10}}\).
Gọi M là hình chiếu của C lên OH.
\( \Rightarrow \cos \left( {\widehat {COH}} \right) = \sin \left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha = - \frac{{\sqrt {19} }}{{10}}\).
Mà \(\cos \widehat {COH} = \frac{{OM}}{{OC}} \Rightarrow - \frac{{\sqrt {19} }}{{10}} = \frac{{OM}}{{OC}} \Rightarrow OM \approx 4,36\,\,\left( m \right)\).
\(\Rightarrow MH = OH - OM = h - OM = 13 - 4,36 = 8,64 m \).
Vậy điểm C cách mặt đất 8,64 m.
Mục 4 của chương trình Toán 11 tập 1 Chân trời sáng tạo tập trung vào các kiến thức về vectơ trong không gian. Đây là một phần quan trọng, đặt nền móng cho các kiến thức hình học nâng cao hơn. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập trong mục này là rất cần thiết để các em có thể giải quyết các bài toán phức tạp hơn trong tương lai.
Trang 17 tập trung vào các bài tập về vectơ trong không gian, đặc biệt là các bài tập về phép cộng, trừ vectơ và nhân với một số thực. Các bài tập này giúp các em làm quen với các phép toán vectơ và rèn luyện kỹ năng tính toán.
Ví dụ: Bài 1 trang 17 yêu cầu tìm vectơ tổng của hai vectơ cho trước. Để giải bài tập này, các em cần áp dụng quy tắc cộng vectơ: cho hai vectơ a = (x1, y1, z1) và b = (x2, y2, z2), thì a + b = (x1 + x2, y1 + y2, z1 + z2).
Trang 18 tập trung vào các bài tập về tích vô hướng của hai vectơ. Các bài tập này giúp các em hiểu rõ hơn về khái niệm tích vô hướng và ứng dụng của nó trong việc tính góc giữa hai vectơ và kiểm tra tính vuông góc.
Ví dụ: Bài 2 trang 18 yêu cầu tính tích vô hướng của hai vectơ cho trước. Để giải bài tập này, các em cần áp dụng công thức tính tích vô hướng: cho hai vectơ a = (x1, y1, z1) và b = (x2, y2, z2), thì a.b = x1x2 + y1y2 + z1z2.
Trang 19 tập trung vào các bài tập về hệ tọa độ trong không gian và ứng dụng của vectơ trong không gian. Các bài tập này giúp các em rèn luyện kỹ năng biểu diễn vectơ, điểm trong không gian bằng tọa độ và giải các bài toán hình học không gian.
Ví dụ: Bài 3 trang 19 yêu cầu tìm tọa độ của một điểm biết tọa độ của các vectơ liên quan. Để giải bài tập này, các em cần sử dụng các công thức liên hệ giữa tọa độ của điểm và tọa độ của các vectơ.
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em sẽ tự tin hơn khi giải bài tập mục 4 trang 17, 18, 19 Toán 11 tập 1 Chân trời sáng tạo. Chúc các em học tốt!