Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2 theo chương trình Chân trời sáng tạo. Mục 2 trang 76 là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
a) Cho đường thẳng (a) song song với mặt phẳng (left( P right)).
a) Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Lấy hai điểm \(A,B\) tuỳ ý trên \(a\) và gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) trên \(\left( P \right)\) (Hình 4a). So sánh độ dài hai đoạn thẳng \(AH\) và \(BK\).
b) Cho hai mặt phẳng song song \(\left( P \right)\) và \(\left( Q \right)\). Lấy hai điểm \(A,B\) tuỳ ý trên \(\left( P \right)\) và gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) trên \(\left( Q \right)\) (Hình 4b). So sánh độ dài hai đoạn thẳng \(AH\) và \(BK\).
Phương pháp giải:
Sử dụng tính chất của phép chiếu vuông góc.
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}AH \bot \left( P \right)\\BK \bot \left( P \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( P \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).
b) Ta có:
\(\left. \begin{array}{l}AH \bot \left( Q \right)\\BK \bot \left( Q \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( Q \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).
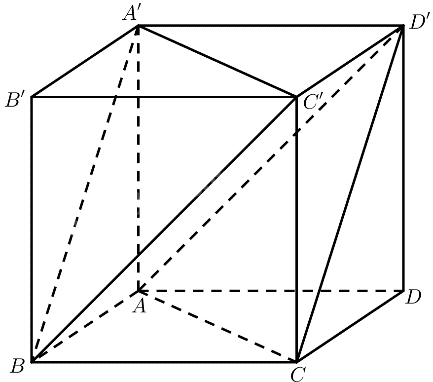
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Tính khoảng cách:
a) Giữa hai mặt phẳng \(\left( {ACD'} \right)\) và \(\left( {A'C'B} \right)\).
b) Giữa đường thẳng \(AB\) và \(\left( {A'B'C'D'} \right)\).
Phương pháp giải:
‒ Cách tính góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) là góc giữa hai đường thẳng lần lượt vuông góc với \(\left( \alpha \right)\) và \(\left( \beta \right)\).
‒ Cách tính góc giữa đường thẳng và mặt phẳng: ta tính góc giữa đường thẳng và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết:

a) \(AA'C'C\) là hình chữ nhật
\(\left. \begin{array}{l} \Rightarrow AC\parallel A'C'\\A'C' \subset \left( {A'C'B} \right)\end{array} \right\} \Rightarrow AC\parallel \left( {A'C'B} \right)\)
\(ABC'D'\) là hình bình hành
\(\left. \begin{array}{l} \Rightarrow AD'\parallel BC'\\BC' \subset \left( {A'C'B} \right)\end{array} \right\} \Rightarrow AD'\parallel \left( {A'C'B} \right)\)
Ta có:
\(\left. \begin{array}{l}AC\parallel \left( {A'C'B} \right)\\AD'\parallel \left( {A'C'B} \right)\\AC,A{\rm{D}}' \subset \left( {AC{\rm{D}}'} \right)\end{array} \right\} \Rightarrow \left( {AC{\rm{D}}'} \right)\parallel \left( {A'C'B} \right) \Rightarrow \left( {\left( {AC{\rm{D}}'} \right),\left( {A'C'B} \right)} \right) = {0^ \circ }\)
b) Ta có:
\(\left. \begin{array}{l}AB\parallel A'B'\\A'B' \subset \left( {A'B'C'D'} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {A'B'C'D'} \right) \Rightarrow \left( {AB,\left( {A'B'C'D'} \right)} \right) = {0^ \circ }\)
Mục 2 trang 76 SGK Toán 11 tập 2 - Chân trời sáng tạo thường tập trung vào các bài toán liên quan đến đạo hàm của hàm số. Cụ thể, các bài tập thường yêu cầu học sinh tính đạo hàm của các hàm số đơn giản, áp dụng quy tắc đạo hàm của tổng, hiệu, tích, thương và hàm hợp. Việc nắm vững các quy tắc này là nền tảng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 2 trang 76, chúng ta sẽ đi vào phân tích từng bài tập cụ thể:
Để tính đạo hàm của hàm số này, ta áp dụng quy tắc đạo hàm của tổng, hiệu và lũy thừa. Ta có:
y' = 3x2 + 4x - 5
Ở đây, ta áp dụng quy tắc đạo hàm của tích. Ta có:
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Ta áp dụng quy tắc đạo hàm của thương. Ta có:
y' = -1/x2
Để tìm đạo hàm của hàm số này, ta áp dụng quy tắc đạo hàm của tổng và đạo hàm của các hàm lượng giác sin(x) và cos(x). Ta có:
y' = cos(x) - sin(x)
Trước tiên, ta tính đạo hàm f'(x) của hàm số f(x):
f'(x) = 2x - 3
Sau đó, ta thay x = 1 vào f'(x) để tính f'(1):
f'(1) = 2(1) - 3 = -1
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Để học tốt môn Toán, đặc biệt là phần đạo hàm, các em cần:
Hy vọng với những chia sẻ trên, các em học sinh sẽ có thêm kiến thức và kỹ năng để giải quyết các bài tập trong mục 2 trang 76 SGK Toán 11 tập 2 - Chân trời sáng tạo một cách hiệu quả. Chúc các em học tập tốt!