Bài 12 trang 128 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 1: Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ, tích vô hướng, và ứng dụng của vectơ trong hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Cho hai hình bình hành (ABCD) và (ABEF) nằm trong hai mặt phẳng khác nhau. Lấy các điểm (M,N) lần lượt thuộc các đường chéo (AC) và (BF) sao cho (MC = 2MA;NF = 2NB). Qua (M,N) kẻ các đường thẳng song song với (AB), cắt các cạnh (AD,AF) lần lượt tại ({M_1},{N_1}). Chứng minh rằng:
Đề bài
Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng khác nhau. Lấy các điểm \(M,N\) lần lượt thuộc các đường chéo \(AC\) và \(BF\) sao cho \(MC = 2MA;NF = 2NB\). Qua \(M,N\) kẻ các đường thẳng song song với \(AB\), cắt các cạnh \(AD,AF\) lần lượt tại \({M_1},{N_1}\). Chứng minh rằng:
a) \(MN\parallel DE\);
b) \({M_1}{N_1}\parallel \left( {DEF} \right)\);
c) \(\left( {MN{N_1}{M_1}} \right)\parallel \left( {DEF} \right)\).
Phương pháp giải - Xem chi tiết
Sử dụng các định lí, tính chất:
‒ Tính chất trọng tâm của tam giác.
‒ Định lí Thalès trong tam giác.
– Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).
‒ Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng \(\left( Q \right)\) thì \(\left( P \right)\) song song với \(\left( Q \right)\).
Lời giải chi tiết
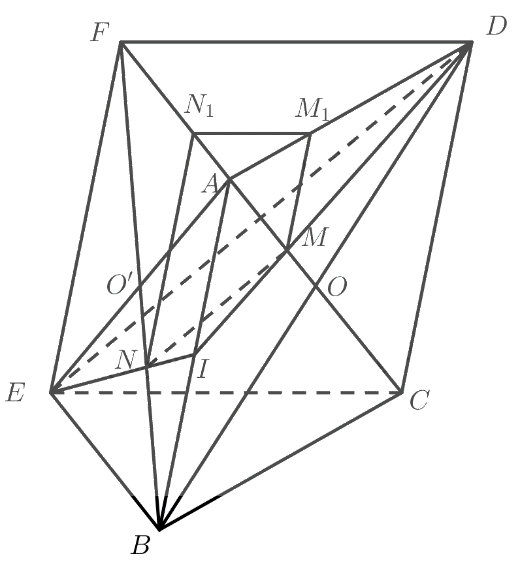
a) Vì AI // CD nên \(\frac{{AI}}{{CD}} = \frac{{IM}}{{MD}} = \frac{{AM}}{{MC}} = \frac{1}{2}\) (định lý Thales).
Vì IB // EF nên \(\frac{{IB}}{{EF}} = \frac{{IN}}{{NE}} = \frac{{BN}}{{NF}} = \frac{1}{2}\) (định lý Thales).
Do đó \(\frac{{IM}}{{MD}} = \frac{{IN}}{{NE}} = \frac{1}{2}\), suy ra MN // DE (định lý Thales đảo).
b) Theo giả thiết, AB // \(M{M_1}\) và \(M{M_1}\) không thuộc (ABEF) nên \(M{M_1}\) // (ABEF).
c) Ta có \(M{M_1}\) // AB // EF, suy ra \(M{M_1}\) // (DEF) (1)
Vì \(N{N_1}\) // AB nên \(\frac{{A{N_1}}}{{{N_1}F}} = \frac{{BN}}{{NF}} = \frac{1}{2}\) (định lý Thales).
Vì \(M{M_1}\) // AB nên \(\frac{{A{M_1}}}{{{M_1}D}} = \frac{{AM}}{{MC}} = \frac{1}{2}\) (định lý Thales).
Do đó \(\frac{{A{N_1}}}{{{N_1}F}} = \frac{{A{M_1}}}{{{M_1}D}} = \frac{1}{2}\), suy ra \({M_1}{N_1}\) // DF và \({M_1}{N_1}\) // (DEF) (2).
Mà \(M{M_1}\) cắt \({M_1}{N_1}\) (3).
Từ (1), (2), (3) suy ra \((MN{N_1}{M_1})\) // (DEF).
Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập tổng hợp, đòi hỏi học sinh phải nắm vững kiến thức về vectơ, tích vô hướng và các ứng dụng của chúng. Dưới đây là giải chi tiết từng phần của bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Ví dụ minh họa:
Cho tam giác ABC có A(1;2), B(3;4), C(5;0). Tính độ dài cạnh AB, BC, CA và xác định loại tam giác ABC.
Giải:
Vì |BC| = |CA| nên tam giác ABC là tam giác cân tại C.
Để nắm vững kiến thức và kỹ năng giải bài tập về vectơ, tích vô hướng và ứng dụng của chúng, bạn nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tìm hiểu thêm về các ứng dụng của vectơ trong các lĩnh vực khác như vật lý, kỹ thuật,...
Các bài tập luyện tập gợi ý:
Khi giải bài tập về vectơ, tích vô hướng và ứng dụng của chúng, bạn cần lưu ý một số điều sau:
Hy vọng với lời giải chi tiết và hướng dẫn trên, bạn đã hiểu rõ cách giải Bài 12 trang 128 SGK Toán 11 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt!