Chào mừng bạn đến với bài học lý thuyết về các công thức lượng giác trong chương trình Toán 11 Chân Trời Sáng Tạo tại giaitoan.edu.vn.
Bài viết này sẽ cung cấp một cách hệ thống và dễ hiểu các công thức lượng giác cơ bản và nâng cao, giúp bạn nắm vững kiến thức nền tảng để giải quyết các bài toán liên quan.
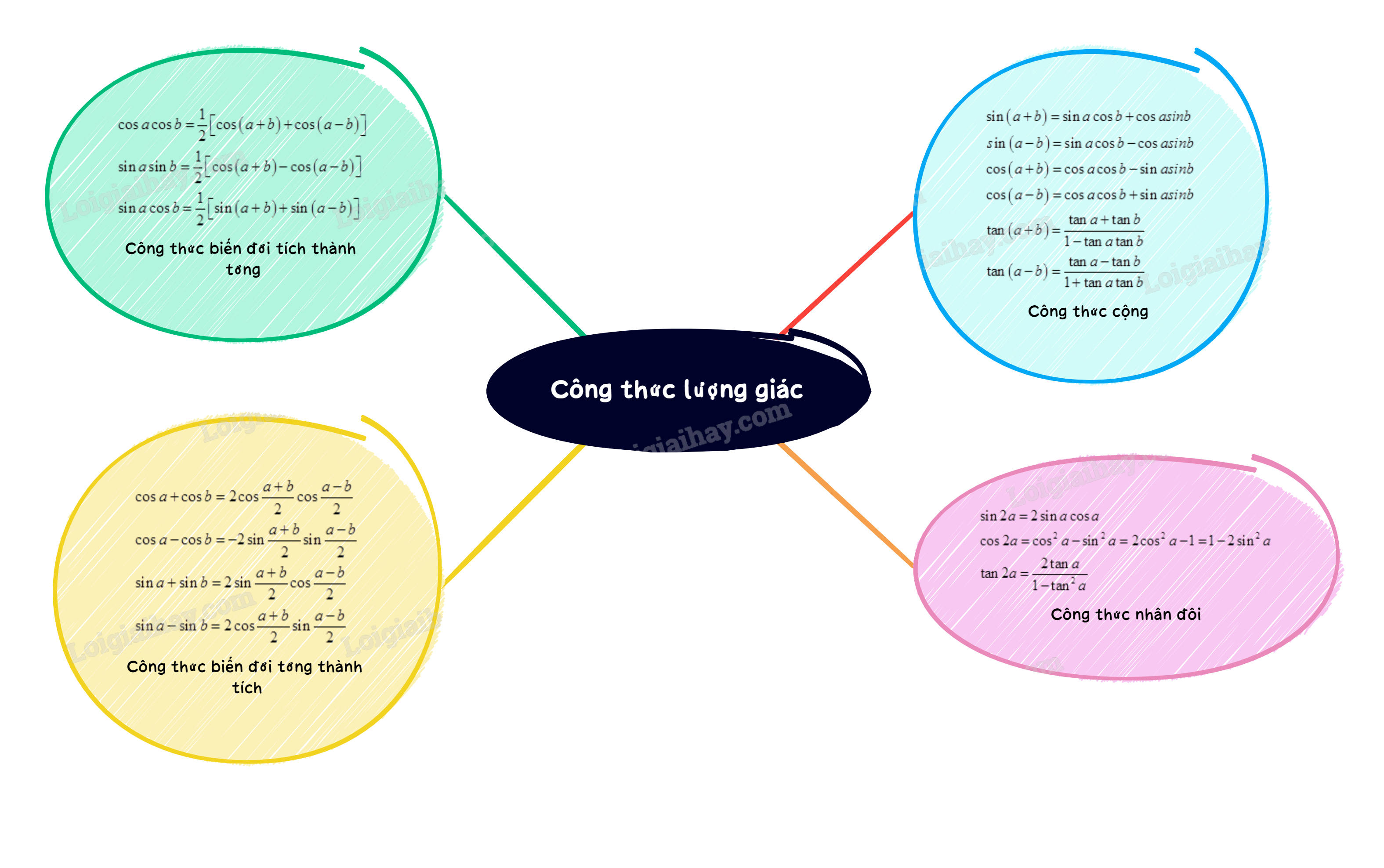
1. Công thức cộng
1. Công thức cộng
\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a - b} \right) = \sin a\cos b - \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b - \sin asinb\\\cos \left( {a - b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\\\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}\end{array}\)
2. Công thức nhân đôi
\(\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\end{array}\)
Suy ra, công thức hạ bậc:
\({\sin ^2}a = \frac{{1 - \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)
3. Công thức biến đổi tích thành tổng
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\end{array}\)
4. Công thức biến đổi tổng thành tích
\(\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\cos a - \cos b = - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\end{array}\)
Lượng giác là một nhánh quan trọng của toán học, nghiên cứu về mối quan hệ giữa các góc và cạnh của tam giác. Trong chương trình Toán 11 Chân Trời Sáng Tạo, học sinh sẽ được làm quen với các khái niệm cơ bản về lượng giác, các hàm số lượng giác và các công thức lượng giác quan trọng.
Các hàm số lượng giác cơ bản bao gồm sin, cos, tan và cot. Chúng được định nghĩa như sau:
Dưới đây là một số công thức lượng giác cơ bản mà học sinh cần nắm vững:
Ngoài các công thức cơ bản, còn có một số công thức lượng giác nâng cao thường được sử dụng trong giải toán:
Các công thức lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học, bao gồm:
Để nắm vững các công thức lượng giác, bạn nên thực hành giải nhiều bài tập khác nhau. Dưới đây là một số dạng bài tập thường gặp:
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và đầy đủ về lý thuyết các công thức lượng giác trong chương trình Toán 11 Chân Trời Sáng Tạo. Chúc bạn học tập tốt!