Chào mừng các em học sinh đến với lời giải chi tiết Bài 9 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo. Bài học này thuộc chương trình đại số lớp 11, tập trung vào các kiến thức về vectơ và ứng dụng trong hình học.
giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là (frac{{2pi }}{3})và số đo góc (OA, OM) là (alpha ).
Đề bài
Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là \(\frac{{2\pi }}{3}\) và số đo góc (OA, OM) là \(\alpha \).
a) Tính sin\(\alpha \) và cos \(\alpha \).
b) Tính sin của các góc lượng giác (OA, ON) và (OA, OP) từ đó tính chiều cao của các điểm N và P so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.

Phương pháp giải - Xem chi tiết
Dựa vào hình vẽ để tìm sin\(\alpha \)và cos \(\alpha \); sử dụng công thức cộng để tính sin của các góc lượng giác (OA, ON) và (OA, OP).
Lời giải chi tiết
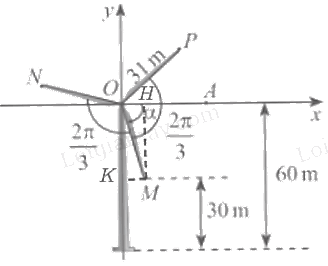
a, Từ điểm M kẻ MH vuông góc với Ox, MK vuông góc với Oy.
Ta có: MH = 60 – 30 = 30 m.
Khi đó hoành độ điểm M là 30.
⇒ \(\;\sin \alpha {\rm{ }} = \;\frac{{MH}}{{OM}} = \;\frac{{30}}{{31}}\)
\( \Rightarrow \cos \alpha = \sqrt {1 - {{\left( {\frac{{30}}{{31}}} \right)}^2}} = \frac{{\sqrt {61} }}{{31}}\)
b, Vì các cánh quạt tạo thành 3 góc bằng nhau nên \(\widehat {MOP} = \widehat {NOP} = \widehat {MON} = {120^0}\)
\( \Rightarrow \widehat {AOP} = \widehat {MOP} - \widehat {MOA}\)
\( \Leftrightarrow \sin \widehat {AOP} = \sin \left( {\widehat {MOP} - \widehat {MOA}} \right) = \sin \widehat {MOP}.\cos \widehat {MOA} - \cos \widehat {MOP}.\sin \widehat {MOA}\)
\( = \sin \frac{{2\pi }}{3}.\cos \alpha - \cos \frac{{2\pi }}{3}.\sin \alpha \approx 0,7\)
Vì vậy chiều cao của điểm P so với mặt đất là:
31. \(\sin \widehat {AOP}\) + 60 = 31.0,7+ 60 \( \approx \) 81,76 m.
Ta có:
\(\cos \widehat {AOP} \approx \sqrt {1 - 0,{7^2}} = 0,71\)
\(\widehat {AON} = \widehat {AOP} + \widehat {PON}\)
\(\begin{array}{l} \Leftrightarrow \sin \widehat {AON} = \sin \left( {\widehat {AOP} + \widehat {PON}} \right)\\ \Leftrightarrow \sin \widehat {AON} = \sin \widehat {AOP}.\cos \widehat {PON} + \cos \widehat {AOP}.\sin \widehat {PON}\\ \Leftrightarrow \sin \widehat {AON} = 0,7.\cos \frac{{2\pi }}{3} + 0,71.\sin \frac{{2\pi }}{3} \approx 0,26\end{array}\)
\( \Rightarrow \sin \left( {OA,ON} \right) = \sin \widehat {AON} \approx 0,26\)
Vì vậy chiều cao của điểm N so với mặt đất là:
31. \(\sin \widehat {AON}\) + 60 = 31.0,26+ 60\( \approx \) 68,2 m.
Bài 9 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học. Cụ thể, bài tập này thường tập trung vào việc chứng minh các đẳng thức vectơ, xác định vị trí tương đối của các điểm, và tính độ dài đoạn thẳng.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải Bài 9 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo, chúng ta cần phân tích kỹ đề bài, xác định các vectơ liên quan, và áp dụng các kiến thức lý thuyết đã học. Dưới đây là hướng dẫn giải chi tiết:
(Nội dung câu a của bài tập)
Lời giải:
(Nội dung câu b của bài tập)
Lời giải:
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, các em có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về vectơ, các em cần lưu ý những điều sau:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập này, các em sẽ nắm vững kiến thức về vectơ và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!
| STT | Nội dung |
|---|---|
| 1 | Định nghĩa vectơ |
| 2 | Các phép toán trên vectơ |
| 3 | Tích vô hướng của hai vectơ |
| Bảng tóm tắt kiến thức | |