Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4 trang 96, 97, 98 sách giáo khoa Toán 11 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?
b) Tìm điểm giống nhau của các hình trong Hình 31.
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình tam giác.
b) Điểm giống nhau của các hình trong Hình 31 là: có các mặt bên là hình tam giác.
Trong Hình 34, hình chóp nào có số mặt ít nhất?

Phương pháp giải:
Quan sát hình ảnh và đếm số mặt của hình.
Lời giải chi tiết:
Hình chóp a) có 4 mặt.
Hình chóp b) có 5 mặt.
Hình chóp c) có 6 mặt.
Hình chóp d) có 7 mặt.
Vậy hình a) có số mặt ít nhất.
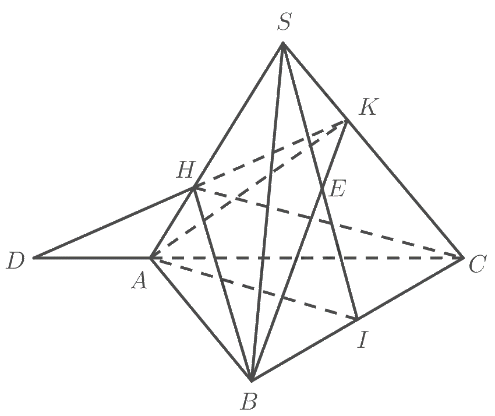
Cho tứ diện \(SABC\). Gọi \(H,K\) lần lượt là hai điểm trên hai cạnh \(SA\) và \(SC\left( {H \ne S,A;K \ne S,C} \right)\) sao cho \(HK\) không song song với \(AC\). Gọi \(I\) là trung điểm của \(BC\) (Hình 38).
a) Tìm giao điểm của đường thẳng \(HK\) và mặt phẳng \(\left( {ABC} \right)\).
b) Tìm giao tuyến của các mặt phẳng \(\left( {SAI} \right)\) và \(\left( {ABK} \right)\); \(\left( {SAI} \right)\) và \(\left( {BCH} \right)\).

Phương pháp giải:
‒ Để tìm giao điểm của đường thẳng và mặt phẳng, ta tìm giao điểm của đường thẳng đó với một đường thẳng trong mặt phẳng.
‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt của hai mặt phẳng đó.
Lời giải chi tiết:

a) Gọi \(D = HK \cap AC\). Ta có:
\(\left. \begin{array}{l}D \in AC \subset \left( {ABC} \right)\\D \in HK\end{array} \right\} \Rightarrow M = HK \cap \left( {ABC} \right)\)
b) Gọi \(E = SI \cap BK\). Ta có:
\(\left. \begin{array}{l}E \in SI \subset \left( {SAI} \right)\\E \in BK \subset \left( {ABK} \right)\end{array} \right\} \Rightarrow E \in \left( {SAI} \right) \cap \left( {ABK} \right)\)
Mà \(A \in \left( {SAI} \right) \cap \left( {ABK} \right)\).
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {ABK} \right)\) là đường thẳng \(AE\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in \left( {SAI} \right)\\I \in BC \subset \left( {BCH} \right)\end{array} \right\} \Rightarrow I \in \left( {SAI} \right) \cap \left( {BCH} \right)\\\left. \begin{array}{l}H \in SA \subset \left( {SAI} \right)\\H \in \left( {BCH} \right)\end{array} \right\} \Rightarrow H \in \left( {SAI} \right) \cap \left( {BCH} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {BCH} \right)\) là đường thẳng \(HI\).
Cho hình chóp \(S.ABCD\). Trên các cạnh bên của hình chóp lấy lần lượt các điểm \(A',B',C',D'\). Cho biết \(AC\) cắt \(B{\rm{D}}\) tại \(O\), \(A'C'\) cắt \(B'{\rm{D'}}\) tại \(O'\), \(AB\) cắt \(DC\) tại \(E\) và \(A'B'\) cắt \(D'C'\) tại \(E'\) (Hình 39). Chứng minh rằng:
a) \(S,O',O\) thẳng hàng;
b) \(S,E',E\) thẳng hàng.

Phương pháp giải:
Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm đó cùng thuộc giao tuyến của hai mặt phẳng.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in BD \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}O' \in A'C' \subset \left( {SAC} \right)\\O' \in B'D' \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O' \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)
Do đó, \(S,O,O'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Vậy \(S,O',O\) thẳng hàng.
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}E \in AB \subset \left( {SAB} \right)\\E \in CD \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\\\left. \begin{array}{l}E' \in A'B' \subset \left( {SAB} \right)\\E' \in C'D' \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow E' \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\end{array}\)
Mà \(S \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\)
Do đó, \(S,E,E'\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SC{\rm{D}}} \right)\).
Vậy \(S,E,E'\) thẳng hàng.
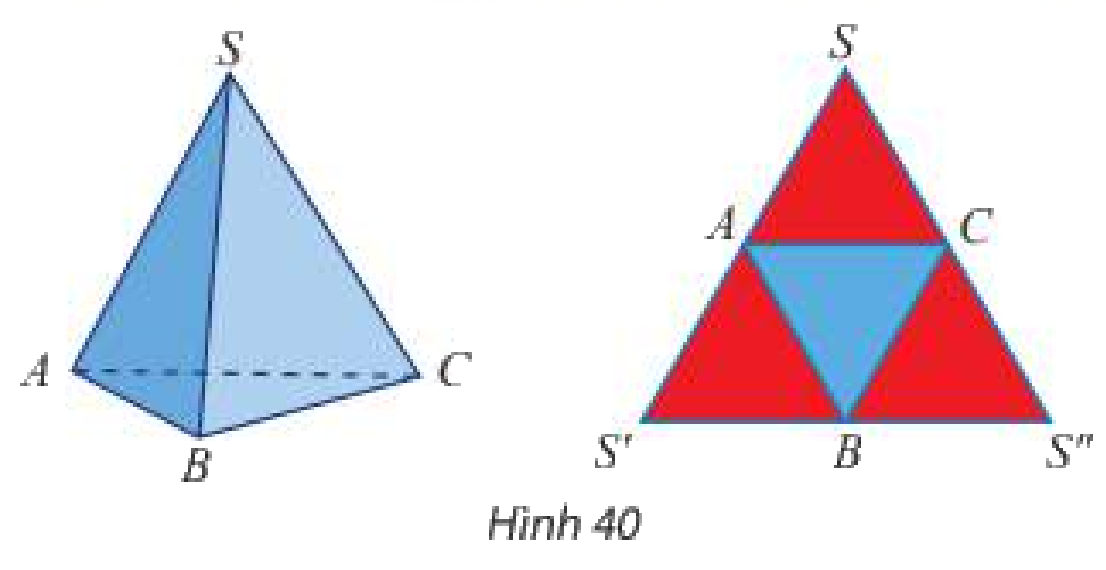
Nêu cách tạo lập tứ diện đều \(SABC\) từ tam giác đều \(SS'S''\) theo gợi ý ở Hình 40.

Phương pháp giải:
Để dựng được tứ diện đều, ta dựng một hình tứ diện có bốn mặt là các tam giác đều.
Lời giải chi tiết:
• Cách dựng:
Bước 1: Gọi \(A,B,C\) lần lượt là trung điểm của \(SS',S'S'',SS''\).
Bước 2: Gấp các đường \(AB,BC,AC\) sao cho các điểm \(S,S',S''\) trùng nhau.
Khi đó, ta được tứ diện đều \(SABC\).
• Chứng minh:
Vì \(A,B,C\) lần lượt là trung điểm của \(SS',S'S'',SS''\) nên theo tính chất đường trung bình của tam giác, ta có: \(SA = S'A = S'B = S''B = SC = S'C = AB = BC = AC = \frac{1}{2}SS'\).
Do vậy các tam giác \(SAC,S'AB,S''BC,ABC\) là các tam giác đều.
Vậy tứ diện \(SABC\) có các mặt \(SAC,SAB,SBC,ABC\) là các tam giác đều nên tứ diện \(SABC\) là tứ diện đều.
Mục 4 của SGK Toán 11 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức về vectơ trong không gian. Các bài tập trong mục này yêu cầu học sinh vận dụng các định nghĩa, tính chất của vectơ, các phép toán vectơ (cộng, trừ, nhân với một số thực) và các ứng dụng của vectơ trong việc giải quyết các bài toán hình học không gian.
Bài tập này giúp học sinh củng cố lại kiến thức cơ bản về vectơ, bao gồm định nghĩa, các loại vectơ, các phép toán vectơ và các tính chất của chúng. Các bài tập thường yêu cầu học sinh thực hiện các phép toán vectơ đơn giản, chứng minh đẳng thức vectơ hoặc xác định các yếu tố của vectơ.
Bài tập này tập trung vào việc tìm hiểu về tích của một vectơ với một số thực. Học sinh sẽ được học về ý nghĩa hình học và đại số của tích vectơ với một số thực, các tính chất của phép nhân vectơ với một số thực và các ứng dụng của phép toán này trong việc giải quyết các bài toán hình học.
Đây là một trong những nội dung quan trọng nhất của chương vectơ trong không gian. Học sinh sẽ được học về định nghĩa của tích vô hướng, các tính chất của tích vô hướng, công thức tính tích vô hướng và các ứng dụng của tích vô hướng trong việc giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài của vectơ, tính vuông góc của hai vectơ.
Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng để giải quyết các bài toán hình học không gian cụ thể, chẳng hạn như tính góc giữa hai đường thẳng, tính khoảng cách từ một điểm đến một đường thẳng, chứng minh các đẳng thức hình học.
Ví dụ: Cho hai vectơ a = (1; 2; 3) và b = (-2; 1; 0). Tính tích vô hướng của hai vectơ này.
Giải: Tích vô hướng của hai vectơ a và b được tính theo công thức:
a.b = xa.xb + ya.yb + za.zb
Thay các giá trị của a và b vào công thức, ta được:
a.b = 1.(-2) + 2.1 + 3.0 = -2 + 2 + 0 = 0
Vậy, tích vô hướng của hai vectơ a và b là 0.
Để học tốt môn Toán 11, các em cần dành thời gian ôn tập lý thuyết thường xuyên, làm nhiều bài tập thực hành và tìm kiếm sự giúp đỡ của giáo viên hoặc bạn bè khi gặp khó khăn. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.