Giải Bài 16 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo

Bài 16 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo

Bài 16 trang 52 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc giải quyết các bài toán liên quan đến đạo hàm của hàm số. Bài tập này giúp học sinh củng cố kiến thức về đạo hàm, ứng dụng đạo hàm để giải quyết các bài toán thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 16 trang 52 SGK Toán 11 tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

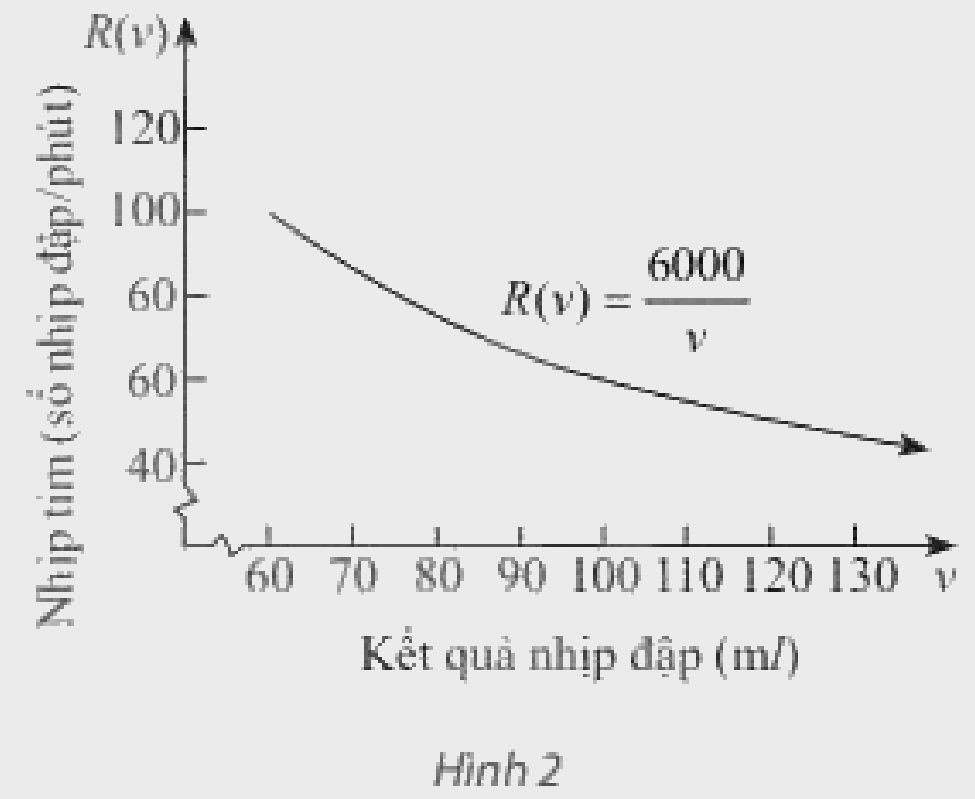
Hàm số (Rleft( v right) = frac{{6000}}{v}) có thể được sử dụng để xác định nhịp tim (R)

Đề bài

Hàm số \(R\left( v \right) = \frac{{6000}}{v}\) có thể được sử dụng để xác định nhịp tim \(R\) của một người mà tim của người đó có thể đây đi được \(6000ml\) máu trên mỗi phút và \(v{\rm{ }}ml\) máu trên mỗi nhịp đập (theo Bách khoa toàn thư Y học “Harrison's internal medicine 21st edition”). Tìm tốc độ thay đổi của nhịp tim khi lượng máu tim đẩy đi ở một nhịp là \(v = 80\).

Bài 16 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiết Bài 16 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo 2

Tính \(R'\left( {80} \right)\).

Lời giải chi tiết

Ta có: \(R'\left( v \right) = 6000.\left( { - \frac{1}{{{v^2}}}} \right) = - \frac{{6000}}{{{v^2}}}\).

Tốc độ thay đổi của nhịp tim khi lượng máu tim đẩy đi ở một nhịp là \(v = 80\) là: \(R'\left( {80} \right) = - \frac{{6000}}{{{{80}^2}}} = - 0,9375\).

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 16 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo – hành trang không thể thiếu trong chuyên mục Giải bài tập Toán 11 trên nền tảng toán học. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 16 trang 52 SGK Toán 11 tập 2 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 16 trang 52 SGK Toán 11 tập 2 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán cụ thể. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập

Bài 16 yêu cầu học sinh thực hiện các thao tác sau:

Tính đạo hàm của các hàm số đã cho.
Xác định khoảng đơn điệu của hàm số.
Tìm cực trị của hàm số.

Lời giải chi tiết

Để giải bài tập này, chúng ta cần nắm vững các công thức và quy tắc về đạo hàm, bao gồm:

Đạo hàm của hàm số lũy thừa.
Đạo hàm của hàm số lượng giác.
Đạo hàm của hàm số hợp.
Quy tắc tính đạo hàm của tích và thương hai hàm số.

Ví dụ: Xét hàm số y = x³ - 3x² + 2.

Tính đạo hàm: y' = 3x² - 6x.
Xác định khoảng đơn điệu:
- y' = 0 khi x = 0 hoặc x = 2.
- Xét dấu y' trên các khoảng (-∞; 0), (0; 2), (2; +∞) để xác định khoảng đồng biến và nghịch biến.
Tìm cực trị:
- Tại x = 0, y' đổi dấu từ dương sang âm, hàm số đạt cực đại.
- Tại x = 2, y' đổi dấu từ âm sang dương, hàm số đạt cực tiểu.

Hướng dẫn giải các bài tập tương tự

Để giải các bài tập tương tự, bạn có thể áp dụng các bước sau:

Xác định hàm số cần tìm đạo hàm.
Sử dụng các công thức và quy tắc đạo hàm để tính đạo hàm của hàm số.
Xác định các điểm mà đạo hàm bằng 0 hoặc không xác định.
Xét dấu đạo hàm trên các khoảng xác định để xác định khoảng đơn điệu của hàm số.
Sử dụng các điểm mà đạo hàm bằng 0 hoặc không xác định để tìm cực trị của hàm số.

Lưu ý quan trọng

Khi giải các bài tập về đạo hàm, bạn cần chú ý các điểm sau:

Nắm vững các công thức và quy tắc đạo hàm.
Kiểm tra kỹ các bước tính toán để tránh sai sót.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm toán học để kiểm tra kết quả.

Ứng dụng của đạo hàm

Đạo hàm có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực khác, bao gồm:

Tìm cực trị của hàm số.
Khảo sát hàm số.
Giải các bài toán tối ưu hóa.
Tính vận tốc và gia tốc trong vật lý.

Hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh có thể tự tin giải Bài 16 trang 52 SGK Toán 11 tập 2 Chân trời sáng tạo và các bài tập tương tự. Chúc các bạn học tốt!

Công thức	Mô tả
(xⁿ)' = nx^n-1	Đạo hàm của hàm số lũy thừa
(sin x)' = cos x	Đạo hàm của hàm số sin x
(cos x)' = -sin x	Đạo hàm của hàm số cos x