Bài 1 trang 64 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Cấp số cho và cấp số nhân. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán liên quan đến cấp số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp (S.ABCD) có (SA bot left( {ABCD} right)).
Đề bài
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Cho biết \(ABCD\) là hình thang vuông tại \(A\) và \({\rm{D}}\), \(AB = 2AD\).
a) Chứng minh \(CD \bot \left( {SAD} \right)\).
b) Gọi \(M\) là trung điểm của \(AB\). Chứng minh \(CM \bot \left( {SAB} \right)\).
Phương pháp giải - Xem chi tiết
Cách chứng minh đường thẳng vuông góc với mặt phẳng: chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
Lời giải chi tiết
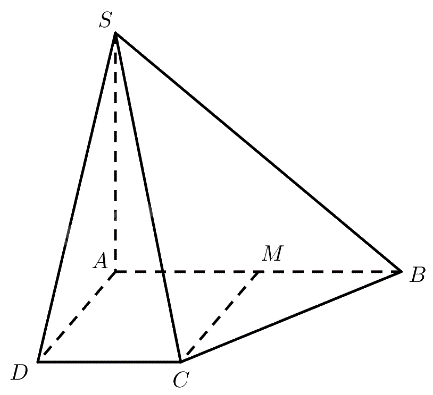
a) Ta có:
\(\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\\AB \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\)
b) Ta có:
\(\left. \begin{array}{l}AB\parallel C{\rm{D}} \Rightarrow AM\parallel C{\rm{D}}\\AM = C{\rm{D}}\left( { = \frac{1}{2}AB} \right)\end{array} \right\}\)
\( \Rightarrow AMC{\rm{D}}\) là hình bình hành
Lại có: \(\widehat {MAD} = {90^ \circ }\)
Vậy \(AMC{\rm{D}}\) là hình chữ nhật
\(\left. \begin{array}{l} \Rightarrow CM \bot AB\\SA \bot \left( {ABCD} \right) \Rightarrow SA \bot CM\end{array} \right\} \Rightarrow CM \bot \left( {SAB} \right)\)
Bài 1 trang 64 SGK Toán 11 tập 2 Chân trời sáng tạo là một bài tập quan trọng trong chương trình ôn tập về cấp số cho và cấp số nhân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức và phương pháp giải liên quan đến hai loại cấp số này.
Bài 1 thường bao gồm các dạng bài tập sau:
Để giải bài 1 trang 64 SGK Toán 11 tập 2, chúng ta cần thực hiện các bước sau:
Giả sử bài tập yêu cầu tìm số hạng thứ 5 của cấp số nhân có số hạng đầu u1 = 2 và công bội q = 3.
Giải:
Số hạng thứ n của cấp số nhân được tính theo công thức: un = u1 * q^(n-1)
Vậy, số hạng thứ 5 của cấp số nhân là: u5 = 2 * 3^(5-1) = 2 * 3^4 = 2 * 81 = 162
Dạng 1: Xác định cấp số
Để xác định một dãy số là cấp số cho hay cấp số nhân, ta cần kiểm tra xem hiệu (trong trường hợp cấp số cho) hoặc thương (trong trường hợp cấp số nhân) giữa hai số hạng liên tiếp có là một hằng số hay không.
Dạng 2: Tìm số hạng tổng quát
Đối với cấp số cho, số hạng tổng quát được tính theo công thức: un = u1 + (n-1)d, trong đó d là công sai.
Đối với cấp số nhân, số hạng tổng quát được tính theo công thức: un = u1 * q^(n-1), trong đó q là công bội.
Dạng 3: Tính tổng của n số hạng đầu tiên
Tổng của n số hạng đầu tiên của cấp số cho được tính theo công thức: Sn = (n/2) * (u1 + un) hoặc Sn = (n/2) * [2u1 + (n-1)d]
Tổng của n số hạng đầu tiên của cấp số nhân được tính theo công thức: Sn = u1 * (1 - q^n) / (1 - q) (với q ≠ 1)
Khi giải các bài tập về cấp số, học sinh cần chú ý các điểm sau:
Cấp số có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 1 trang 64 SGK Toán 11 tập 2 Chân trời sáng tạo và các bài tập tương tự. Chúc các em học tốt!