Chào mừng bạn đến với bài học về Lý thuyết Hai mặt phẳng song song, một phần quan trọng trong chương trình Toán 11 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và nâng cao về hai mặt phẳng song song, các điều kiện để hai mặt phẳng song song, và ứng dụng của lý thuyết này trong giải các bài toán hình học không gian.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu, cùng với hệ thống bài tập đa dạng để bạn có thể tự tin chinh phục môn Toán.
1. Hai mặt phẳng song song
1. Hai mặt phẳng song song
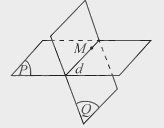
Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm chung.
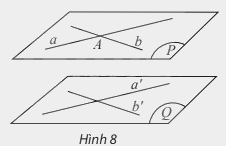
2. Điều kiện để hai mặt phẳng song song
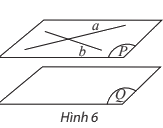
3. Tính chất của hai mặt phẳng song song
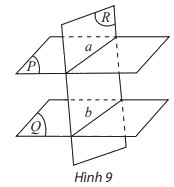
4. Định lí Thalès trong không gian
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.
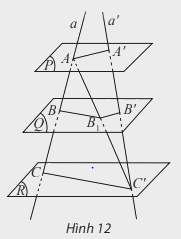
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\)
5. Hình lăng trụ và hình hộp
- Cho hai mặt phẳng song song \(\left( P \right)\) và \(\left( {P'} \right)\). Trên \(\left( P \right)\) cho đa thức đa giác lồi \({A_1}{A_2}...{A_n}\). Qua các đỉnh\({A_1},{A_2},...,{A_n}\)vẽ các đường thẳng đôi một song song và cắt mặt phẳng \(\left( {P'} \right)\)tại \({A_1}',{A_2}',...,{A_n}'\). Hình gồm hai đa giác\({A_1}{A_2}...{A_n}\), \({A_1}'{A_2}'...{A_n}'\) và các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\)được gọi là hình lăng trụ và kí hiệu là \({A_1}{A_2}...{A_n}.{A_1}'{A_2}'...{A_n}'\).
- Các điểm \({A_1},{A_2},...,{A_n}\) và \({A_1}',{A_2}',...,{A_n}'\)được gọi là các đỉnh, các đoạn thẳng \({A_1}{A_1}',{A_2}{A_2}',...,{A_n}{A_n}'\)được gọi là các cạnh bên, các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_n}{A_1}\)và \({A_1}'{A_2}',{A_2}'{A_3}',...,{A_n}'{A_1}'\) gọi là cạnh đáy của hình trụ.
- Hai đa giác \({A_1}{A_2}...{A_n}\)và \({A_1}'{A_2}'...{A_n}'\)được gọi là hai mặt đáy của hình lăng trụ.
Các tứ giác \({A_1}{A_1}'{A_2}'{A_2}\),\({A_2}{A_2}'{A_3}'{A_3}\),…,\({A_n}{A_n}'{A_1}'{A_1}\) gọi là các mặt bên của hình trụ.
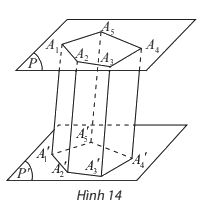
- Hình lăng trụ có đáy là tam giác, tứ giác, ngũ giác,…tương ứng được gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác,…
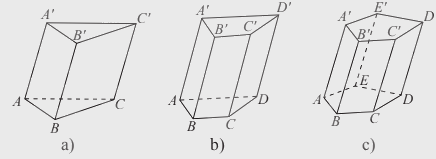
- Hình hộp là hình lăng trụ có đáy là hình bình hành.
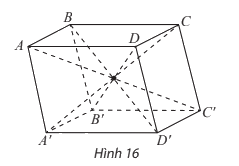
- Trong hình hình hộp có:
+ Sáu mặt là sau hình bình hành. Mỗi mặt đều có một mặt song song với nó gọi là haimặt đối diện.
+ Hai đỉnh không cùng nằm trưn một mặt gọi là hai đỉnh đối diện.
+ Đoạn thẳng nối 2 đỉnh đối diện gọi là đường chéo.
+ Bốn đường chéo cắt nhau tại trung điểm mỗi đường.
Trong hình học không gian, việc hiểu rõ về mối quan hệ giữa các mặt phẳng là vô cùng quan trọng. Một trong những mối quan hệ cơ bản nhất là quan hệ song song giữa hai mặt phẳng. Bài viết này sẽ trình bày chi tiết về lý thuyết hai mặt phẳng song song theo chương trình Toán 11 Chân trời sáng tạo, bao gồm định nghĩa, điều kiện nhận biết, và các tính chất quan trọng.
Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung. Ký hiệu: (P) // (Q). Điều này có nghĩa là khi kéo dài vô hạn, hai mặt phẳng này không bao giờ giao nhau.
Có một số điều kiện để xác định hai mặt phẳng song song:
Hai mặt phẳng song song có những tính chất sau:
Lý thuyết hai mặt phẳng song song được ứng dụng rộng rãi trong việc giải các bài toán hình học không gian, đặc biệt là trong việc chứng minh các mối quan hệ giữa các yếu tố hình học. Ví dụ:
Bài tập 1: Cho hình chóp S.ABCD. Đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng mặt phẳng (SAD) song song với mặt phẳng (BCM).
Giải:
Ta có M là trung điểm của CD, suy ra MD = MC. Vì ABCD là hình vuông nên AD // BC. Do đó, AD // MC. Mặt khác, AD nằm trong (SAD) và MC nằm trong (BCM). Vậy (SAD) // (BCM) theo điều kiện 1.
Để hiểu sâu hơn về lý thuyết hai mặt phẳng song song, bạn có thể tìm hiểu thêm về:
Lý thuyết hai mặt phẳng song song là một phần kiến thức quan trọng trong chương trình Toán 11 Chân trời sáng tạo. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán hình học không gian một cách hiệu quả và chính xác. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và đầy đủ về chủ đề này.