Chào mừng bạn đến với bài học về Lý thuyết Góc lượng giác trong chương trình Toán 11 Chân trời sáng tạo tại giaitoan.edu.vn. Góc lượng giác là một phần quan trọng của chương trình, đặt nền móng cho các kiến thức hình học và lượng giác nâng cao hơn.
Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan về các khái niệm cơ bản, công thức quan trọng và các ứng dụng thực tế của góc lượng giác, giúp bạn tự tin giải quyết các bài tập trong SGK và các đề thi.
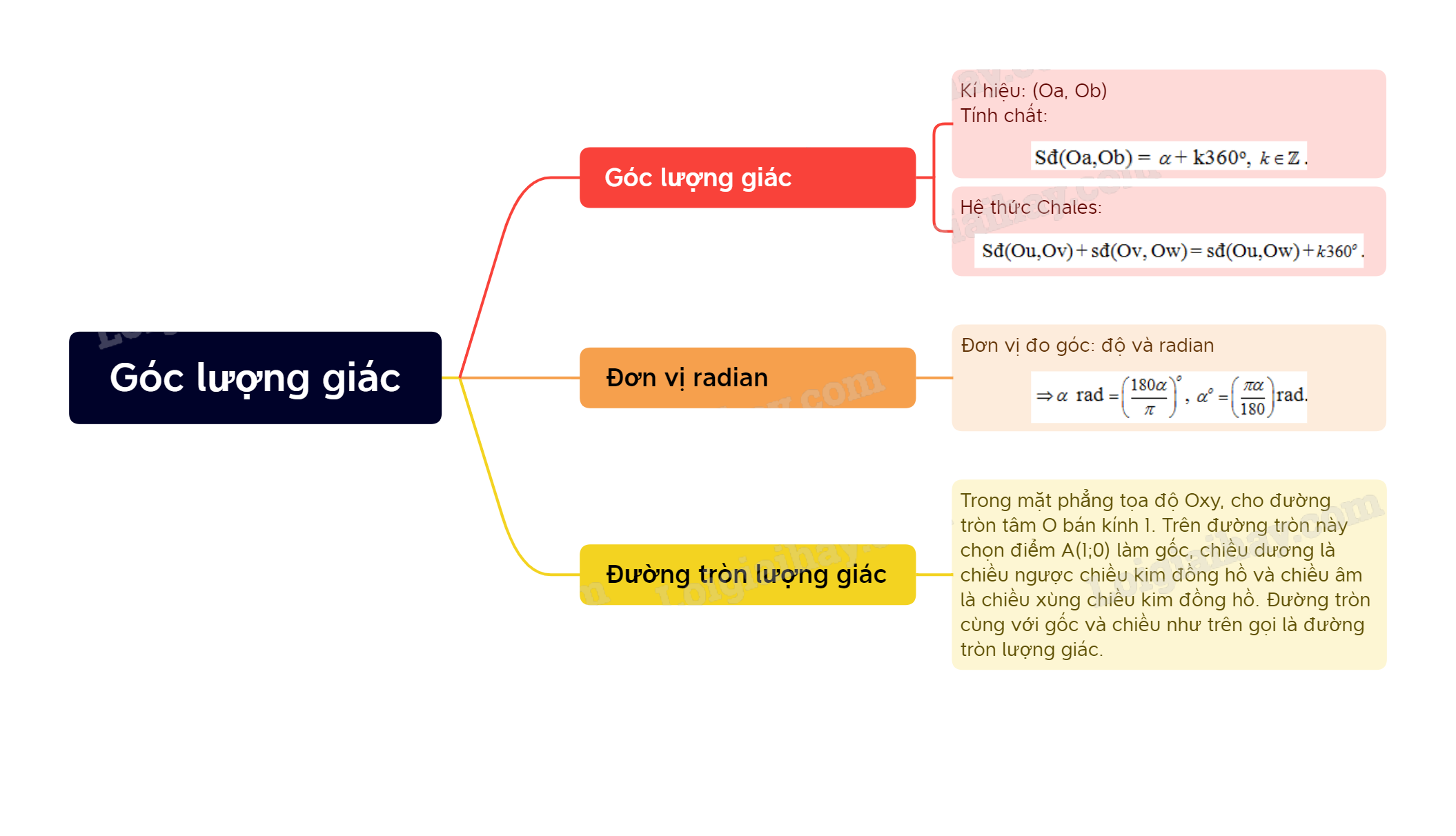
1. Góc lượng giác
1. Góc lượng giác
* Khái niệm góc lượng giác
- Cho 2 tia Oa, Ob.
Nếu tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob.
Kí hiệu: (Oa, Ob).
- Khi tia Om quay một góc \(\alpha \) ta nói số đo của góc lượng giác (Oa, Ob) bằng \(\alpha \), kí hiệu sđ(Oa, Ob) =\(\alpha \)
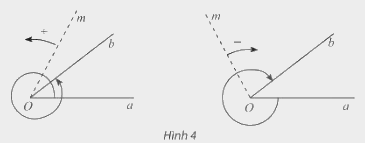
* Chú ý:
- Với 2 tia Oa, Ob cho trước, có vô số góc lượng giác tia đầu Oa, tia cuối Ob. Ta dùng chung kí hiệu (Oa, Ob) cho tất cả các góc lượng giác này.
- Số đo các góc lượng giác có cùng tia đầu Oa, tia cuối Ob sai khác nhau một bội nguyên của 360o có công thức là:
Sđ(Oa,Ob) = \(\alpha \)+ k360o, \(k \in \mathbb{Z}\).
* Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
Sđ(Ou,Ov) + sđ(Ov, Ow) = sđ(Ou,Ow) +k360o, \(k \in \mathbb{Z}\).
2. Đơn vị radian
Trên đường tròn bán kính R tùy ý, góc ở tâm chắn một cung có độ dài đúng bằng R được gọi là một góc có số đo 1 radian (rad).
Ta có: \({180^o} = \pi \)rad, do đó 1 rad \( = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \left( {\frac{\pi }{{180}}} \right)\)rad.
\( \Rightarrow \alpha \) rad \( = {\left( {\frac{{180\alpha }}{\pi }} \right)^o}\), \({\alpha ^o} = \left( {\frac{{\pi \alpha }}{{180}}} \right)\)rad.
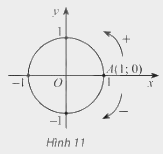
3. Đường tròn lượng giác
Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm O bán kính 1. Trên đường tròn này chọn điểm A(1;0) làm gốc, chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là chiều xùng chiều kim đồng hồ. Đường tròn cùng với gốc và chiều như trên gọi là đường tròn lượng giác.
Góc lượng giác là một khái niệm quan trọng trong toán học, đặc biệt là trong chương trình Toán 11 Chân trời sáng tạo. Nó mở rộng định nghĩa về góc từ hình học phẳng sang các góc có số đo lớn hơn 360 độ, và cung cấp một công cụ mạnh mẽ để giải quyết các bài toán liên quan đến đường tròn lượng giác và các hàm lượng giác.
Trong mặt phẳng tọa độ Oxy, một góc lượng giác α được xác định bởi hai tia Om và On. Tia Om là tia gốc, tia On là tia cuối. Số đo của góc lượng giác α được tính bằng độ (°) hoặc radian (rad). Chiều dương của việc quay là ngược chiều kim đồng hồ.
Đường tròn lượng giác là đường tròn đơn vị (bán kính bằng 1) có tâm tại gốc tọa độ O. Mỗi điểm M trên đường tròn lượng giác được xác định bởi một góc lượng giác α, sao cho góc xOM bằng α.
Các hàm số lượng giác (sin, cos, tan, cot) là các hàm số liên kết góc lượng giác α với các tỷ số giữa các cạnh của tam giác vuông đơn vị. Cụ thể:
| Góc α | sin α | cos α | tan α | cot α |
|---|---|---|---|---|
| 0° (0 rad) | 0 | 1 | 0 | Không xác định |
| 30° (π/6 rad) | 1/2 | √3/2 | √3/3 | √3 |
| 45° (π/4 rad) | √2/2 | √2/2 | 1 | 1 |
| 60° (π/3 rad) | √3/2 | 1/2 | √3 | √3/3 |
| 90° (π/2 rad) | 1 | 0 | Không xác định | 0 |
Các công thức lượng giác là các đẳng thức liên hệ giữa các hàm số lượng giác. Một số công thức quan trọng bao gồm:
Biến đổi lượng giác là quá trình sử dụng các công thức lượng giác để đưa biểu thức lượng giác về dạng đơn giản hơn hoặc để giải các phương trình lượng giác. Các công thức cộng, trừ, nhân, chia góc, công thức hạ bậc, nâng bậc là những công cụ quan trọng trong biến đổi lượng giác.
Góc lượng giác có nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn toàn diện về lý thuyết Góc lượng giác trong chương trình Toán 11 Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài tập.