Bài 14 trang 42 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán liên quan đến hàm số bậc hai, đồ thị hàm số và ứng dụng của hàm số trong thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 14 trang 42 SGK Toán 11 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
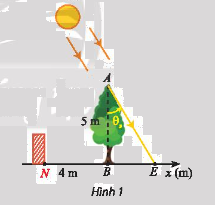
Trong Hình 1, cây xanh AB nằm trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao 5 m.
Đề bài
Trong Hình 1, cây xanh AB nằm trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao 5 m. Bóng của cây là BE. Vào ngày xuân phân và hạ phân, điểm E di chuyển trên đường thẳng Bx. Góc thiên đỉnh \({\theta _t} = (AB,AE)\) phụ thuộc vào vị trí của Mặt trời và thay đổi theo thời gian trong ngày theo công thức \({\theta _s}(t) = (AB,AE) = \frac{\pi }{{12}}(t - 12)\;\) rad với t là thời gian trong ngày (theo đơn vị giờ, 6 < t < 18).
(Theo https://www.sciencedirect.com/topics/engineering/solar-hour-angle)
a) Viết hàm số biểu diễn toạ độ của điểm E trên trục Bx theo t.
b) Dựa vào đồ thị hàm số tang, hãy xác định các thời điểm mà tại đó bóng cây phủ qua vị trí tường rào N biết N nằm trên trục Bx với toạ độ là \({x_N} = - 4\;\) (m). Làm tròn kết quả đến hàng phần mười.
Phương pháp giải - Xem chi tiết
a, Dựa vào hình vẽ để viết hàm số biểu diễn tọa độ điểm E.
b, Giải bất phương trình để tìm ra t.
Lời giải chi tiết
a) Xét tam giác ABE vuông tại B, có:
\(tan{\theta _s}(t) = \frac{{BE}}{{AB}} \Leftrightarrow BE = 5tan\left( {\frac{\pi }{{12}}(t - 12)} \right)\)
b) Đồ thị của hàm số \({\theta _s} = 5tan\left( {\frac{\pi }{{12}}(t - 12)} \right)\)
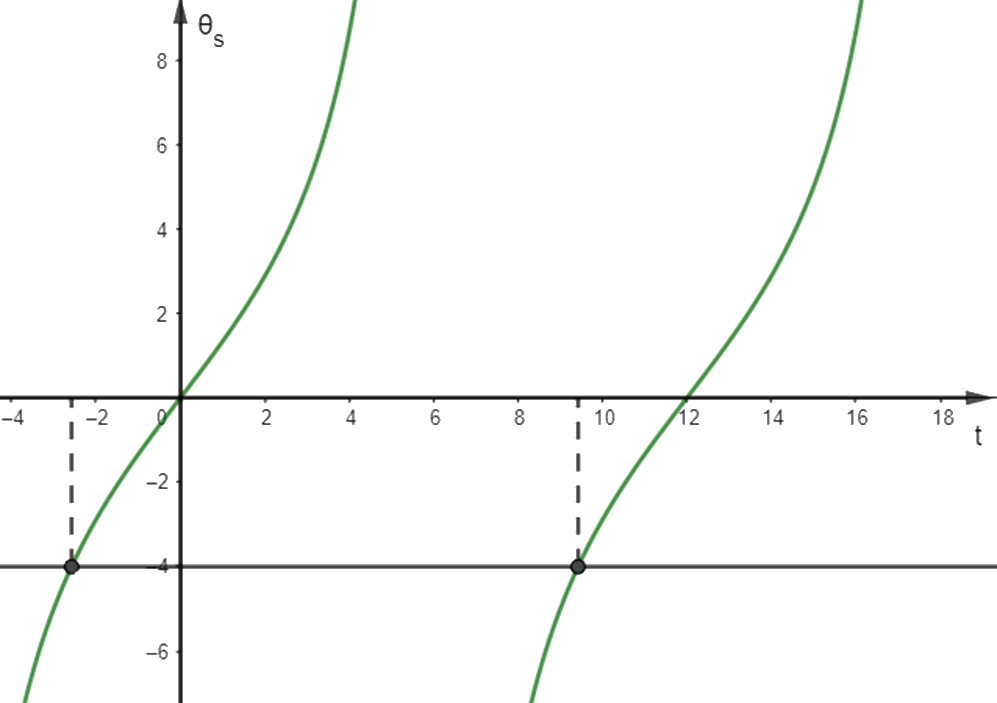
Dựa vào đồ thị hàm số để \({\theta _s} = 5tan\left( {\frac{\pi }{{12}}(t - 12)} \right) < - 4\)
\(\begin{array}{l} \Leftrightarrow tan\left( {\frac{\pi }{{12}}(t - 12)} \right) < - \frac{4}{5}\\ \Leftrightarrow \frac{\pi }{{12}}(t - 12) < - 0,67\\ \Leftrightarrow t < 9,4\end{array}\)
Kết hợp điều kiện \(6 < t < 18 \Rightarrow 6 < t < 9,4\).
Vậy thời điểm bóng cây phủ qua hàng rào là 6 < t < 9,4.
Bài 14 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số bậc hai và ứng dụng của nó. Dưới đây là giải chi tiết và hướng dẫn giải bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
(Ở đây sẽ là nội dung giải chi tiết từng câu hỏi của bài 14, bao gồm các bước giải, giải thích rõ ràng và sử dụng các ví dụ minh họa. Ví dụ:)
Câu a: Xác định hệ số a, b, c của hàm số y = 2x2 - 5x + 3.
Giải: Ta có a = 2, b = -5, c = 3.
Câu b: Tìm tọa độ đỉnh của parabol.
Giải: x0 = -(-5)/(2*2) = 5/4. y0 = 2*(5/4)2 - 5*(5/4) + 3 = -7/8. Vậy đỉnh của parabol là I(5/4, -7/8).
Câu c: Vẽ đồ thị hàm số.
Giải: (Hướng dẫn các bước vẽ đồ thị, bao gồm xác định các điểm đặc biệt, vẽ trục đối xứng và vẽ parabol).
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:
Kiến thức về hàm số bậc hai có ứng dụng rất lớn trong thực tế, ví dụ như:
Bài 14 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc hai và ứng dụng của nó. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc hai | y = ax2 + bx + c (a ≠ 0) |
| Đỉnh của parabol | I(x0, y0) với x0 = -b/2a |