Bài học này cung cấp kiến thức nền tảng về số trung bình và mốt trong thống kê, đặc biệt áp dụng cho mẫu số liệu ghép nhóm. Chúng ta sẽ tìm hiểu cách tính toán và ý nghĩa của các đại lượng này trong việc phân tích dữ liệu.
Nội dung bài học được trình bày chi tiết, dễ hiểu, phù hợp với chương trình SGK Toán 11 Chân trời sáng tạo. Học sinh sẽ được làm quen với các công thức và phương pháp tính toán thực tế.
1. Số liệu ghép nhóm
1. Số liệu ghép nhóm
- Mẫu số liệu ghép nhóm là thường được trình bày dưới dạng bảng thống kê có dạng như sau:
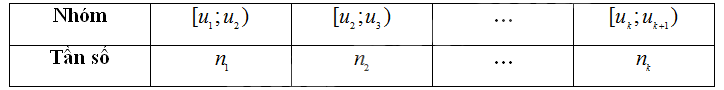
Bảng 1. Bảng tần số ghép nhóm
- Bảng trên gồm k nhóm \({\rm{[}}{u_i};{u_{i + 1}})\) với \(1 \le j \le k\), mỗi nhóm gồm một số giá trị được ghép theo một tiêu chí xác định.
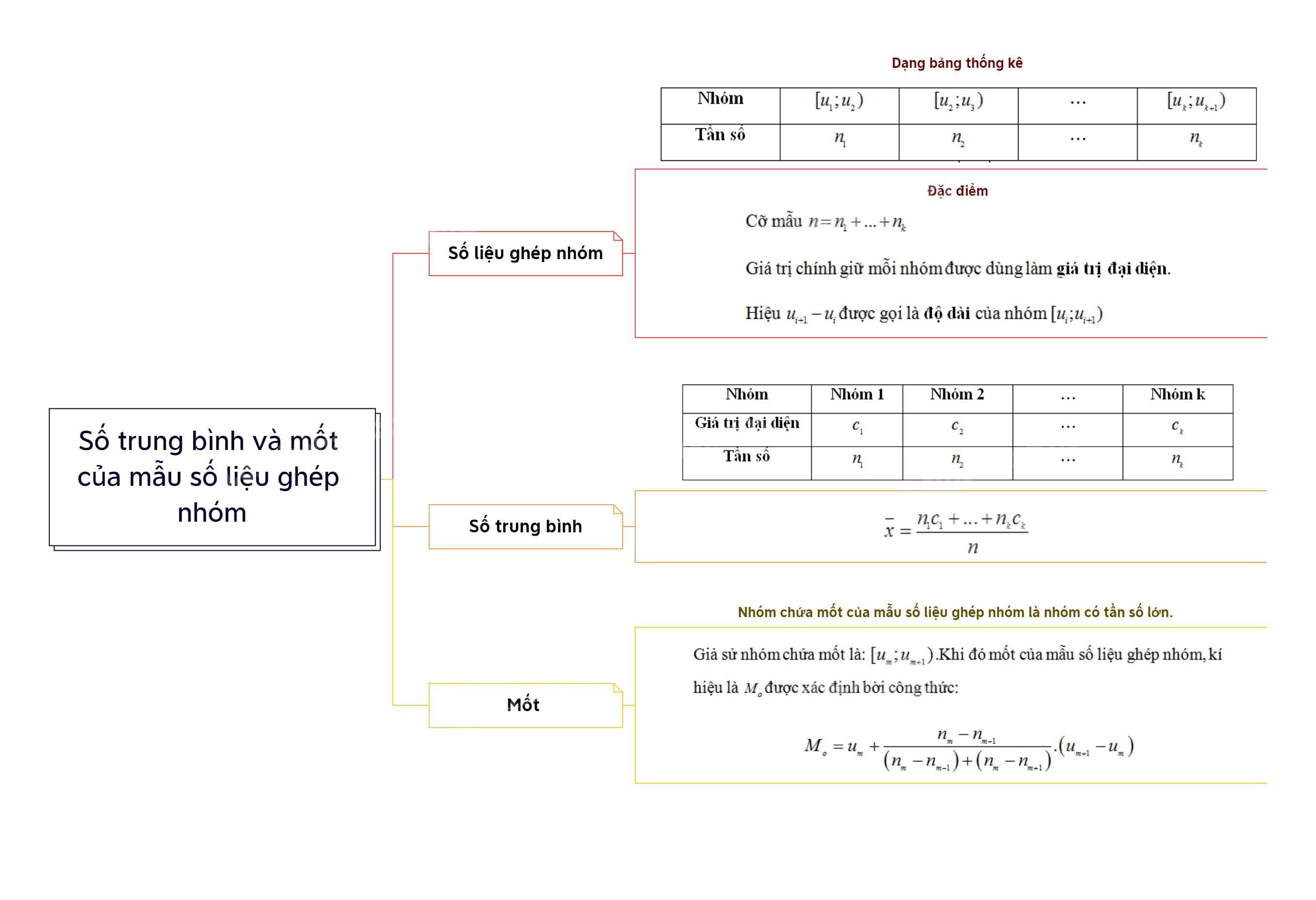
- Cỡ mẫu \(n = {n_1} + ... + {n_k}\)
- Giá trị chính giữa mỗi nhóm được dùng làm giá trị đại diện.
- Hiệu \({u_{i + 1}} - {u_i}\) được gọi là độ dài của nhóm \({\rm{[}}{u_i};{u_{i + 1}})\)
- Sử dụng từ \(k = 5\) đến \(k = 20\) nhóm. Cỡ mẫu càng lớn thì cần càng nhiều nhóm số liệu.
- Các nhóm có cùng độ dài bằng L thỏa mãn R < k.L, trong đó R là khoảng biến thiên, k là số nhóm.
- Giá trị nhỏ nhất của mẫu thuộc vào nhóm\({\rm{[}}{u_1};{u_2})\) và càng gần \({u_1}\) càng tốt. Giá trị lớn nhất của mẫu thuộc nhóm \({\rm{[}}{u_k};{u_{k + 1}})\) và càng gần \({u_{k + 1}}\) càng tốt.
* Chú ý:
Các đầu mút của nhóm có thể không là giá trị của mẫu số liệu.
2. Số trung bình

Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\overline x \) được tính như sau:
\(\overline x = \frac{{{n_1}{c_1} + ... + {n_k}{c_k}}}{n}\)
Trong đó, \(n = {n_1} + ... + {n_k}\) là cỡ mẫu.
Ý nghĩa: Số trung bình của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho số trung bình của mẫu số liệu gốc. Nó thường dùng để đo xu thế trung tâm của mẫu số liệu.
3. Mốt
- Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn nhất.
Giả sử nhóm chứa mốt là: \({\rm{[}}{u_m};{u_{m + 1}})\). Khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_o}\) được xác định bời công thức:
\({M_o} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
- Nếu không có nhóm kề trước của nhóm chứa mốt thì \({n_{m - 1}} = 0\). Nếu không có nhóm kề sau của nhóm chứa mốt thì \({n_{m + 1}} = 0\).
- Mốt của mẫu số liệu ghép nhóm là giá trị có khả năng xuất hiện cao nhất khi lấy mẫu. Mốt của mẫu số liệu sau khi ghép nhóm \({M_o}\) xấp xỉ với mốt của mẫu số liệu không ghép nhóm. Các giá trị nằm xung quanh \({M_o}\) thường có khả năng xuất hiện cao hơn các giá trị khác.
- Một mẫu số liệu ghép nhóm có thể không có mốt hoặc có nhiều hơn một mốt.
Trong thống kê, việc tóm tắt và mô tả dữ liệu là vô cùng quan trọng. Số trung bình và mốt là hai đại lượng thống kê cơ bản, giúp chúng ta hiểu rõ hơn về xu hướng tập trung của một tập dữ liệu. Bài viết này sẽ đi sâu vào lý thuyết về số trung bình và mốt của mẫu số liệu ghép nhóm, theo chương trình SGK Toán 11 Chân trời sáng tạo.
Mẫu số liệu ghép nhóm là một cách trình bày dữ liệu, trong đó các giá trị được chia thành các khoảng (nhóm) và chỉ số lượng các giá trị trong mỗi khoảng được ghi lại. Ví dụ, thay vì liệt kê chiều cao của từng học sinh, chúng ta có thể nhóm thành các khoảng như 150-155cm, 155-160cm, v.v., và ghi lại số lượng học sinh trong mỗi khoảng.
Số trung bình (hay trung bình cộng) của mẫu số liệu ghép nhóm được tính theo công thức:
x̄ = (∑(xi * ni)) / N
Trong đó:
Ví dụ: Giả sử chúng ta có bảng tần số sau:
| Khoảng | Trung điểm (xi) | Tần số (ni) |
|---|---|---|
| 10-15 | 12.5 | 5 |
| 15-20 | 17.5 | 8 |
| 20-25 | 22.5 | 7 |
Số trung bình sẽ là: x̄ = ((12.5 * 5) + (17.5 * 8) + (22.5 * 7)) / (5 + 8 + 7) = (62.5 + 140 + 157.5) / 20 = 360 / 20 = 18
Mốt (mode) của mẫu số liệu ghép nhóm là khoảng có tần số lớn nhất. Nói cách khác, mốt là khoảng chứa nhiều giá trị nhất trong mẫu.
Ví dụ: Trong bảng tần số ở trên, khoảng 15-20 có tần số lớn nhất (8), do đó mốt của mẫu số liệu là khoảng 15-20.
Số trung bình cho biết giá trị trung tâm của mẫu số liệu. Nó là một đại lượng đo lường xu hướng tập trung của dữ liệu.
Mốt cho biết giá trị xuất hiện nhiều nhất trong mẫu. Nó giúp chúng ta xác định giá trị phổ biến nhất trong dữ liệu.
Số trung bình và mốt được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, bao gồm:
| Khoảng | Tần số |
|---|---|
| 5-10 | 3 |
| 10-15 | 7 |
| 15-20 | 5 |
| 20-25 | 2 |
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết số trung bình và mốt của mẫu số liệu ghép nhóm. Hãy luyện tập thêm các bài tập để nắm vững kiến thức này và áp dụng vào thực tế.