Chào mừng bạn đến với bài học về Lý thuyết Phép tính lũy thừa trong chương trình Toán 11 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về lũy thừa, giúp bạn giải quyết các bài toán một cách hiệu quả.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất và các ứng dụng của phép tính lũy thừa, đồng thời luyện tập thông qua các ví dụ minh họa cụ thể.
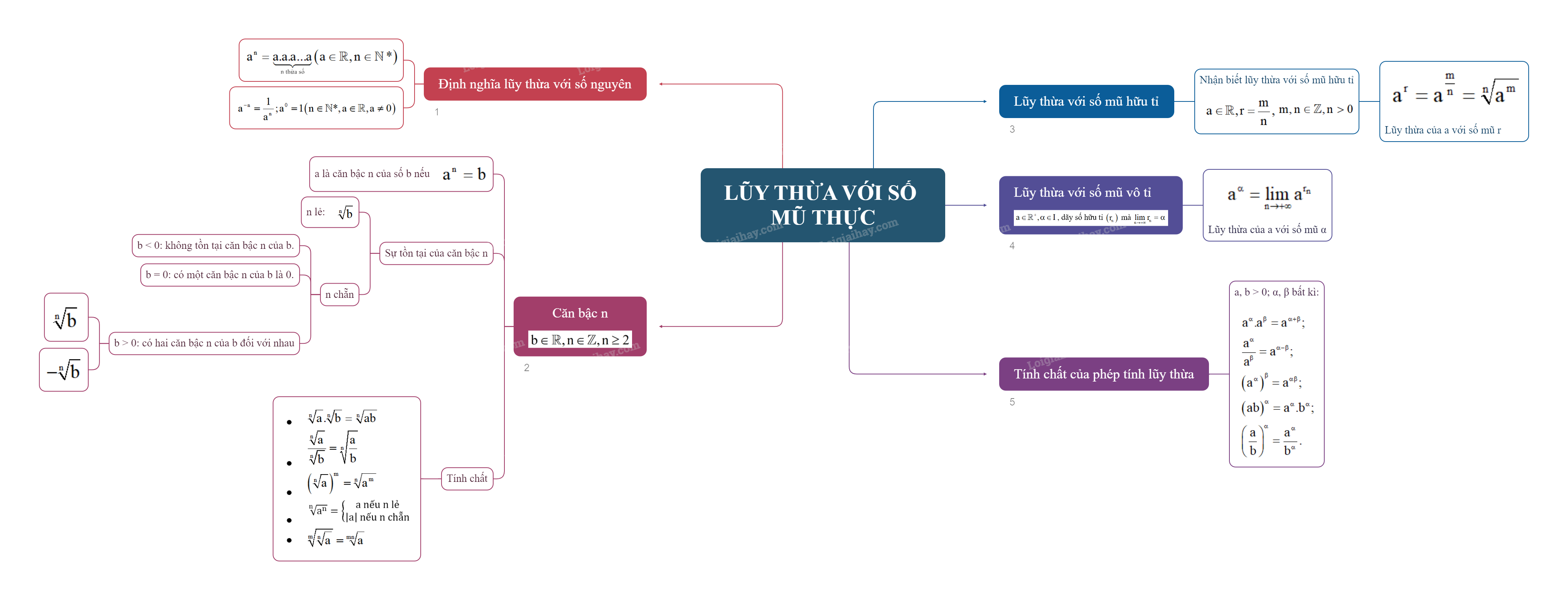
1. Lũy thừa với số mũ nguyên - Lũy thừa với số mũ nguyên dương:
1. Lũy thừa với số mũ nguyên
- Lũy thừa với số mũ nguyên dương:
\({a^n} = \underbrace {a.a.a...a}_{n\,thừa\,số}\left( {a \in \mathbb{R},n \in \mathbb{N}*} \right)\).
- Lũy thừa với số mũ nguyên âm, số mũ 0:
\({a^{ - n}} = \frac{1}{{{a^n}}};{a^0} = 1\left( {n \in \mathbb{N}*,a \in \mathbb{R},a \ne 0} \right)\).
2. Căn bậc n
Cho số thực b và số nguyên \(n \ge 2\).
- Số a là căn bậc n của số b nếu \({a^n} = b\).
- Sự tồn tại căn bậc n:
+ Nếu n lẻ thì có duy nhất một căn bậc n của b, kí hiệu \(\sqrt[n]{b}\).
+ Nếu n chẵn thì:
+ Các tính chất:
3. Lũy thừa với số mũ hữu tỉ
Cho số thực dương a và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m,n \in \mathbb{Z},n > 0\). Ta có:
\({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\)
4. Lũy thừa với số mũ vô tỉ
Giả sử a là một số dương, \(\alpha \) là một số vô tỉ và \(\left( {{r_n}} \right)\) là một dãy số hữu tỉ sao cho \(\lim {r_n} = \alpha \). Khi đó \({a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } = {a^{{r_n}}}\).
5. Tính chất của phép tính lũy thừa
Cho a, b là những số thực dương; \(\alpha ;\beta \) là những số thực bất kì. Khi đó:
\(\begin{array}{l}{a^\alpha }.{a^\beta } = {a^{\alpha + \beta }};\\\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha - \beta }};\\{\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha \beta }};\\{\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha };\\{\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}.\end{array}\)
Phép tính lũy thừa là một trong những khái niệm cơ bản và quan trọng trong toán học, đặc biệt là trong chương trình Toán 11. Hiểu rõ lý thuyết và vận dụng thành thạo các công thức liên quan đến lũy thừa sẽ giúp học sinh giải quyết các bài toán một cách nhanh chóng và chính xác.
Lũy thừa của một số thực a (cơ số) với số mũ nguyên dương n là tích của n thừa số bằng a, ký hiệu là an. Trong đó:
Ví dụ: 23 = 2 × 2 × 2 = 8
Phép tính lũy thừa có nhiều tính chất quan trọng, bao gồm:
Lũy thừa với số mũ hữu tỉ được định nghĩa như sau:
Ví dụ: 81/3 = 2 (căn bậc ba của 8 bằng 2)
Trong chương trình Toán 11 Chân trời sáng tạo, các bài tập về phép tính lũy thừa thường gặp các dạng sau:
Ví dụ 1: Tính giá trị của biểu thức 2-3 × 42
Giải:
2-3 × 42 = 2-3 × (22)2 = 2-3 × 24 = 2-3+4 = 21 = 2
Ví dụ 2: Rút gọn biểu thức (a2b-1)3
Giải:
(a2b-1)3 = (a2)3 × (b-1)3 = a6 × b-3 = a6 / b3
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Phép tính lũy thừa - Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!