Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 80, 81 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học và hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 11 và đạt kết quả cao trong học tập.
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}1&{khi\,\,0 \le x \le 1}\\{1 + x}&{khi\,\,1 < x \le 2}\\{5 - x}&{khi\,\,2 < x \le 3}\end{array}} \right.\) có đồ thị như Hình 1.
Cho hàm số \(y = f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}1&{khi\,\,0 \le x \le 1}\\{1 + x}&{khi\,\,1 < x \le 2}\\{5 - x}&{khi\,\,2 < x \le 3}\end{array}} \right.\) có đồ thị như Hình 1.
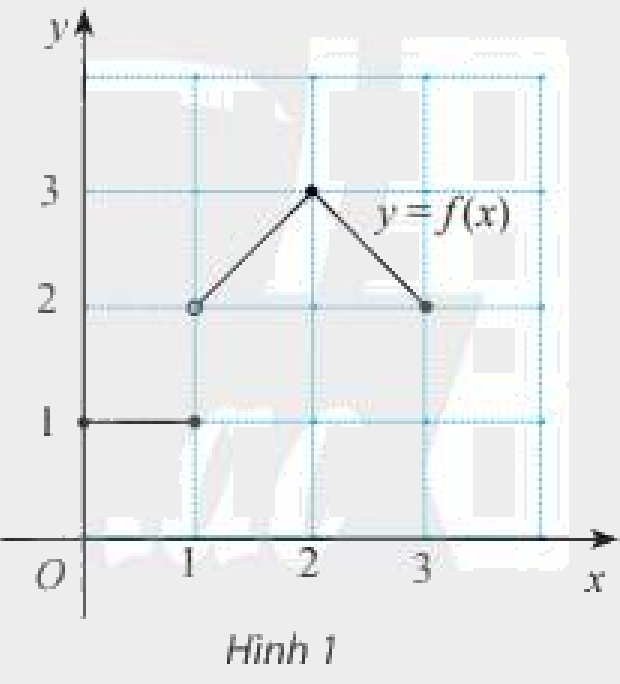
Tại mỗi điểm \({x_0} = 1\) và \({x_0} = 2\), có tồn tại giới hạn \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) không? Nếu có, giới hạn đó có bằng \(f\left( {{x_0}} \right)\) không?
Phương pháp giải:
Bước 1: Tính các giới hạn một bên \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right),\mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right)\).
Bước 2: So sánh \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right),\mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right)\)
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right) = L\) thì \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\).
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x \right) \ne \mathop {\lim }\limits_{x \to {x_0}^ - } {\rm{ }}f\left( x \right)\) thì không tồn tại \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\).
Lời giải chi tiết:
• \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {1 + x} \right) = 1 + 1 = 2\).
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} 1 = 1\).
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).
• \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {5 - x} \right) = 5 - 2 = 3\).
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {1 + x} \right) = 1 + 2 = 3\).
Vì \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} {\rm{ }}f\left( x \right) = 3\) nên \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 3\).
Ta có: \(f\left( 2 \right) = 1 + 2 = 3\).
Vậy \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\).
Xét tính liên tục của hàm số:
a) \(f\left( x \right) = 1 - {x^2}\) tại điểm \({x_0} = 3\);
b) \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{x^2} + 1}&{khi\,\,x > 1}\\{ - x}&{khi\,\,x \le 1}\end{array}} \right.\) tại điểm \({x_0} = 1\).
Phương pháp giải:
Bước 1: Kiểm tra \({x_0}\) thuộc tập xác định. Tính \(f\left( {{x_0}} \right)\).
Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) (nếu có).
Bước 3: Kết luận:
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\) thì hàm số liên tục tại điểm \({x_0}\).
• Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) \ne f\left( {{x_0}} \right)\) hoặc không tồn tại \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right)\) thì hàm số không liên tục tại điểm \({x_0}\).
Lời giải chi tiết:
a) \(f\left( 3 \right) = 1 - {3^2} = 1 - 9 = - 8\).
\(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \left( {1 - {x^2}} \right) = 1 - {3^2} = 1 - 9 = - 8\).
Vì \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right) = - 8\) nên hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0} = 3\).
b) \(f\left( 1 \right) = - 1\).
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} + 1} \right) = {1^2} + 1 = 2\).
\(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - x} \right) = - 1\).
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} {\rm{ }}f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\)
Vậy hàm số không liên tục tại điểm \({x_0} = 1\).
Mục 1 của chương trình Toán 11 tập 1 Chân trời sáng tạo tập trung vào việc giới thiệu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, mở đầu cho chương trình Giải tích. Việc hiểu rõ khái niệm này sẽ giúp học sinh tiếp cận các kiến thức phức tạp hơn trong tương lai.
Bài tập này yêu cầu học sinh vận dụng định nghĩa và các tính chất của giới hạn để tính giới hạn của các hàm số đơn giản. Ví dụ:
lim (x→2) (x2 + 1)
Giải: Thay x = 2 vào hàm số, ta được: 22 + 1 = 5. Vậy lim (x→2) (x2 + 1) = 5.
Bài tập này yêu cầu học sinh xác định giới hạn của hàm số khi x tiến tới vô cùng dương hoặc vô cùng âm. Ví dụ:
lim (x→+∞) (1/x)
Giải: Khi x tiến tới vô cùng dương, 1/x tiến tới 0. Vậy lim (x→+∞) (1/x) = 0.
Bài tập này yêu cầu học sinh kết hợp các tính chất của giới hạn để giải quyết các bài toán phức tạp hơn. Ví dụ:
lim (x→1) (x2 - 1) / (x - 1)
Giải: Ta có thể phân tích tử số thành (x - 1)(x + 1). Vậy lim (x→1) (x2 - 1) / (x - 1) = lim (x→1) (x + 1) = 2.
Khái niệm giới hạn có nhiều ứng dụng trong thực tế, chẳng hạn như trong việc tính tốc độ tức thời, gia tốc, diện tích dưới đường cong, và trong các bài toán về tối ưu hóa.
Việc nắm vững kiến thức về giới hạn là rất quan trọng đối với học sinh lớp 11. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài toán về giới hạn.