Chào mừng các em học sinh đến với lời giải chi tiết Bài 1 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo. Bài học này thuộc chương trình Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến phép đếm và các quy tắc tổ hợp cơ bản.
giaitoan.edu.vn cung cấp lời giải dễ hiểu, chi tiết, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự. Hãy cùng chúng tôi khám phá lời giải ngay sau đây!
Vẽ đồ thị các hàm số sau:
Đề bài
Vẽ đồ thị các hàm số sau:
a) \(y = {4^x}\);
b) \(y = {\left( {\frac{1}{4}} \right)^x}\).
Phương pháp giải - Xem chi tiết
Lập bảng giá trị, dựa vào bảng giá trị vẽ đồ thị.
Lời giải chi tiết
a) Bảng giá trị:
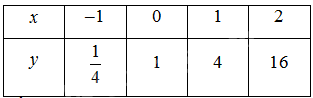
Đồ thị:
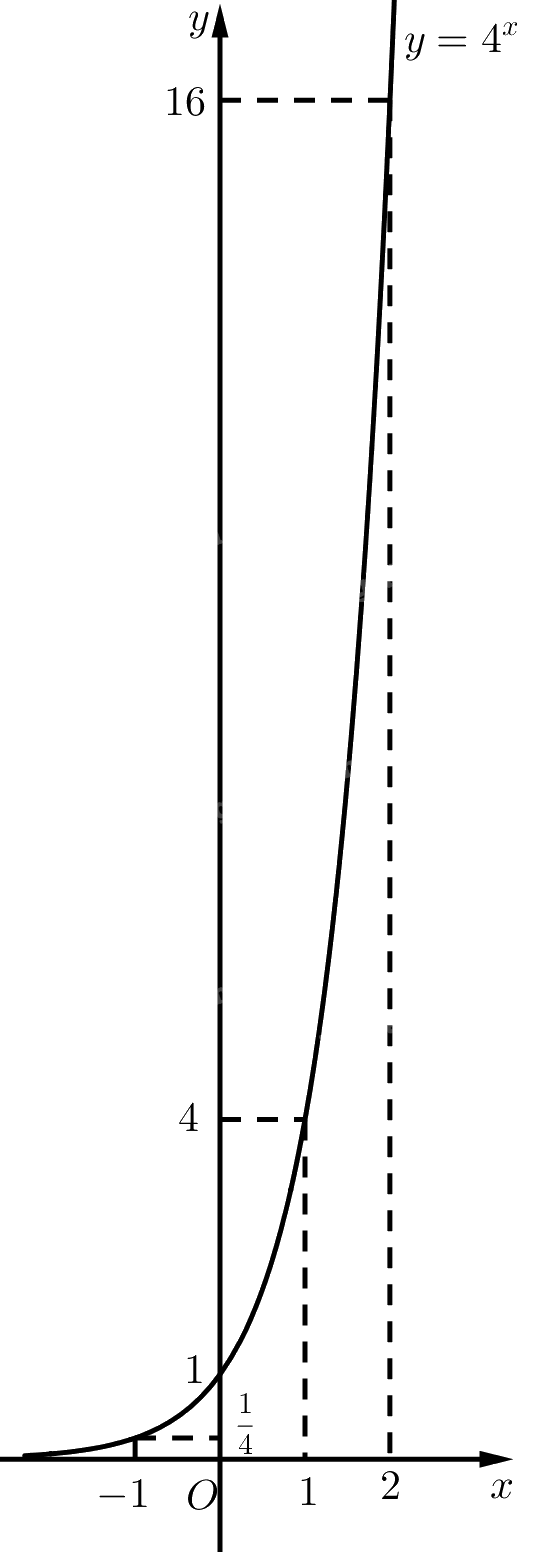
b) Bảng giá trị:
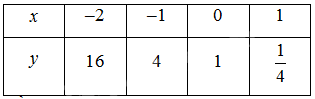
Đồ thị:
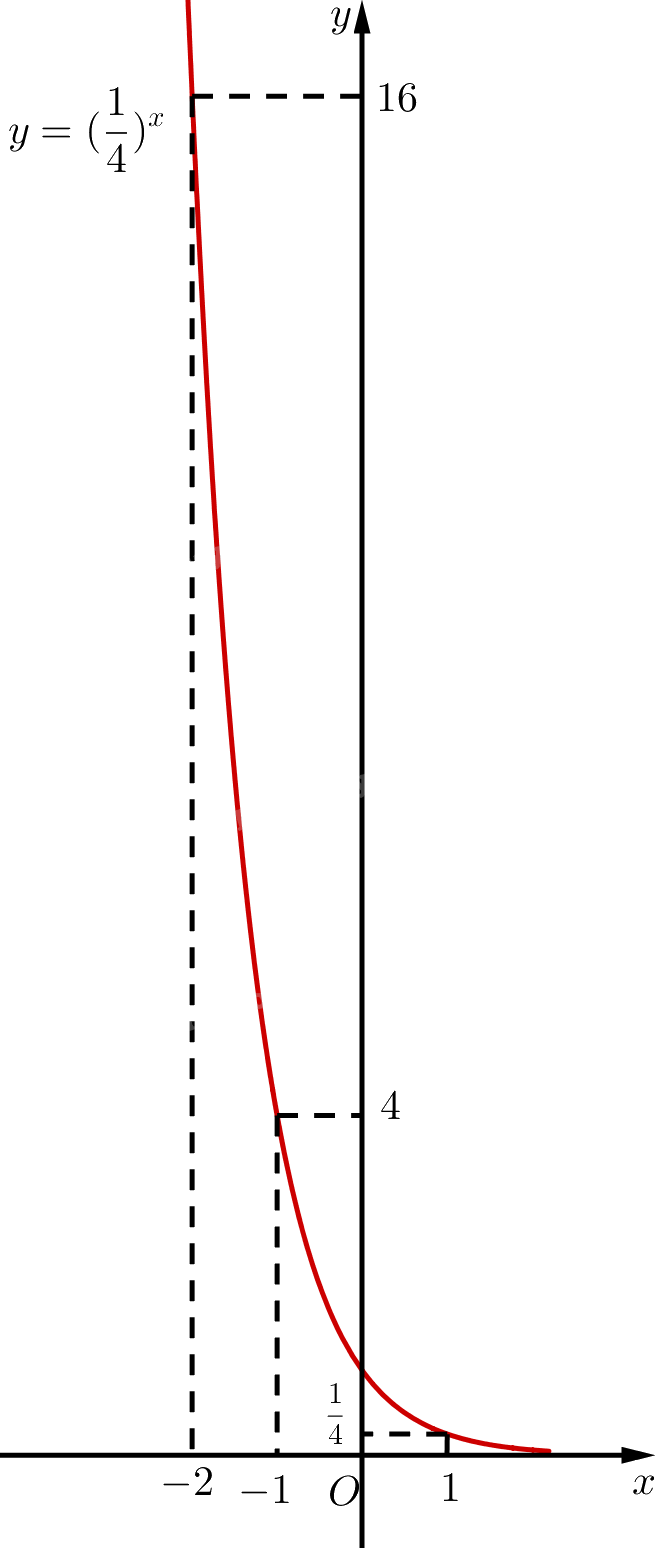
Bài 1 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về hoán vị, chỉnh hợp và tổ hợp để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết cho từng phần của bài tập:
Trong phần này, học sinh cần xác định số cách sắp xếp các phần tử khác nhau theo một thứ tự nhất định. Để giải bài toán này, ta sử dụng công thức hoán vị: P(n) = n!
Ví dụ, nếu có 5 cuốn sách khác nhau, số cách sắp xếp chúng trên một kệ sách là P(5) = 5! = 120.
Chỉnh hợp là việc sắp xếp một số phần tử lấy từ một tập hợp lớn hơn theo một thứ tự nhất định. Công thức chỉnh hợp là: A(n, k) = n! / (n-k)!
Ví dụ, nếu có 10 học sinh và cần chọn ra 3 học sinh để xếp vào ba vị trí khác nhau (ví dụ: lớp trưởng, lớp phó học tập, lớp phó văn thể), số cách chọn là A(10, 3) = 10! / 7! = 720.
Tổ hợp là việc chọn một số phần tử từ một tập hợp lớn hơn mà không quan tâm đến thứ tự. Công thức tổ hợp là: C(n, k) = n! / (k! * (n-k)!)
Ví dụ, nếu có 8 quả bóng khác nhau và cần chọn ra 3 quả, số cách chọn là C(8, 3) = 8! / (3! * 5!) = 56.
Một hội nghị có 10 người tham gia, trong đó có 5 nam và 5 nữ. Hỏi có bao nhiêu cách chọn ra một ban đại diện gồm 3 người, trong đó có ít nhất 1 người nam?
Để giải bài toán này, ta có thể tính tổng số cách chọn 3 người từ 10 người, sau đó trừ đi số cách chọn 3 người đều là nữ.
Tổng số cách chọn 3 người từ 10 người là C(10, 3) = 120.
Số cách chọn 3 người đều là nữ là C(5, 3) = 10.
Vậy số cách chọn ban đại diện có ít nhất 1 người nam là 120 - 10 = 110.
Bài 1 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hoán vị, chỉnh hợp và tổ hợp. Việc nắm vững các công thức và kỹ năng giải bài tập sẽ giúp các em tự tin hơn trong các kỳ thi và ứng dụng kiến thức vào thực tế.
giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập và đạt kết quả tốt trong học tập.