Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 84 và 85 sách giáo khoa Toán 11 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
Cho hai mặt phẳng (left( P right)) và (left( Q right)) cắt nhau theo giao tuyến (d).
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\). Hãy gọi tên các nửa mặt phẳng có chung bờ \(d\). Các nửa mặt phẳng này chia không gian thành bao nhiêu phần?

Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
Các nửa mặt phẳng có chung bờ \(d\) là: \(\left( {{P_1}} \right),\left( {{P_2}} \right),\left( {{Q_1}} \right),\left( {{Q_2}} \right)\).
Các nửa mặt phẳng này chia không gian thành 4 phần.
Cho góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\). Gọi \(O\) là một điểm tuỳ ý trên \(d\). \(Ox\) là tia nằm trong \(\left( P \right)\) và vuông góc với \(d\), \(Oy\) là tia nằm trong \(\left( Q \right)\) và vuông góc với \(d\) (Hình 6).
a) Nêu nhận xét về vị trí tương đối giữa \(d\) và \(mp\left( {Ox,Oy} \right)\).
b) Nêu nhận xét về số đo của góc \(xOy\) khi \(O\) thay đổi trên \(d\).

Phương pháp giải:
Sử dụng định lí: Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}d \bot Ox\\d \bot Oy\end{array} \right\} \Rightarrow d \bot mp\left( {Ox,Oy} \right)\)
b) Số đo của góc \(xOy\) không đổi khi \(O\) thay đổi trên \(d\).
Cho hình chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy và có tất cả các cạnh đều bằng \(a\). Xác định và tính góc phẳng nhị diện:
a) \(\left[ {S,BC,O} \right]\);
b) \(\left[ {C,SO,B} \right]\).
Phương pháp giải:
‒ Cách xác định góc phẳng nhị diện \(\left[ {A,d,B} \right]\): Dựng mặt phẳng \(\left( P \right)\) vuông góc với \(d\), gọi \(a,a'\) lần lượt là giao tuyến của \(\left( P \right)\) với hai nửa mặt phẳng chứa \(A,B\), khi đó \(\left[ {A,d,B} \right] = \left( {a,a'} \right)\).
Lời giải chi tiết:

a) Gọi \(H\) là trung điểm của \(BC\).
\(\Delta SBC\) đều \( \Rightarrow SH \bot BC\)
\(\Delta OBC\) vuông cân tại \(O \Rightarrow OH \bot BC\)
Vậy \(\widehat {SHO}\) là góc phẳng nhị diện \(\left[ {S,BC,O} \right]\).
Ta có: \(O\) là trung điểm của \(BD\)
\(H\) là trung điểm của \(BC\)
\( \Rightarrow OH\) là đường trung bình của \(\Delta BC{\rm{D}}\)
\( \Rightarrow OH = \frac{1}{2}CD = \frac{a}{2}\)
\(AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SOH\) vuông tại \(O\) có: \(SO = \sqrt {S{C^2} - O{C^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\tan \widehat {SHO} = \frac{{SO}}{{OH}} = \sqrt 2 \Rightarrow \widehat {SHO} \approx 54,{7^ \circ }\)
b) Ta có:
\(\begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OB\\SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC\end{array}\)
Vậy \(\widehat {BOC}\) là góc phẳng nhị diện \(\left[ {C,SO,B} \right]\).
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow \widehat {BOC} = {90^ \circ }\).
Cho biết kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98 m và cạnh đáy 180 m. Tính số đo góc nhị diện tạo bởi mặt bên và mặt đáy.
(Nguồn: https://en.wikipedia.org/wiki/Memphis Pyramid)

Phương pháp giải:
Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
Lời giải chi tiết:
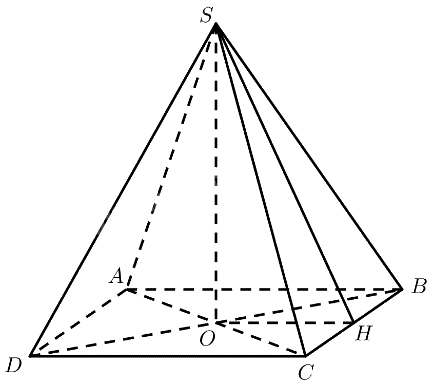
Mô hình hoá kim tự tháp bằng chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy. Vậy \(AB = 180,SO = 98\)
Gọi \(H\) là trung điểm của \(BC\).
\(\Delta SBC\) đều \( \Rightarrow SH \bot BC\)
\(\Delta OBC\) vuông cân tại \(O \Rightarrow OH \bot BC\)
Vậy \(\widehat {SHO}\) là góc nhị diện tạo bởi mặt bên và mặt đáy.
Ta có: \(O\) là trung điểm của \(BD\)
\(H\) là trung điểm của \(BC\)
\( \Rightarrow OH\) là đường trung bình của \(\Delta BC{\rm{D}}\)
\( \Rightarrow OH = \frac{1}{2}CD = 90\)
\(\tan \widehat {SHO} = \frac{{SO}}{{OH}} = \frac{{49}}{{45}} \Rightarrow \widehat {SHO} \approx 47,{4^ \circ }\)
Vậy số đo góc nhị diện tạo bởi mặt bên và mặt đáy là \(47,{4^ \circ }\).
Mục 2 của chương trình Toán 11 tập 2, Chân trời sáng tạo thường tập trung vào các kiến thức về đạo hàm của hàm số. Cụ thể, các em sẽ được học về ý nghĩa của đạo hàm, các quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán liên quan đến đạo hàm trong các chương tiếp theo.
Các bài tập trong mục 2 trang 84, 85 SGK Toán 11 tập 2 thường yêu cầu học sinh:
Để tính đạo hàm của hàm số f(x) = x^3 + 2x^2 - 5x + 1, ta áp dụng quy tắc tính đạo hàm của tổng và quy tắc tính đạo hàm của lũy thừa:
f'(x) = (x^3)' + (2x^2)' - (5x)' + (1)'
f'(x) = 3x^2 + 4x - 5 + 0
f'(x) = 3x^2 + 4x - 5
Để tính đạo hàm của hàm số g(x) = (x^2 + 1) / (x - 1), ta áp dụng quy tắc tính đạo hàm của thương:
g'(x) = [(x^2 + 1)'(x - 1) - (x^2 + 1)(x - 1)'] / (x - 1)^2
g'(x) = [2x(x - 1) - (x^2 + 1)(1)] / (x - 1)^2
g'(x) = (2x^2 - 2x - x^2 - 1) / (x - 1)^2
g'(x) = (x^2 - 2x - 1) / (x - 1)^2
Để tìm hệ số góc của tiếp tuyến của đường cong y = x^2 tại điểm có hoành độ x = 2, ta tính đạo hàm của hàm số y = x^2 và thay x = 2 vào đạo hàm đó:
y' = (x^2)' = 2x
Hệ số góc của tiếp tuyến tại x = 2 là: y'(2) = 2 * 2 = 4
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 84, 85 SGK Toán 11 tập 2, chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!