Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 75, 76 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học toán online hiệu quả, tiết kiệm thời gian và đạt kết quả tốt nhất.
Cho hàm số \(f\left( x \right) = \frac{1}{x}\) có đồ thị như Hình 3.
Cho hàm số \(f\left( x \right) = \frac{1}{x}\) có đồ thị như Hình 3.
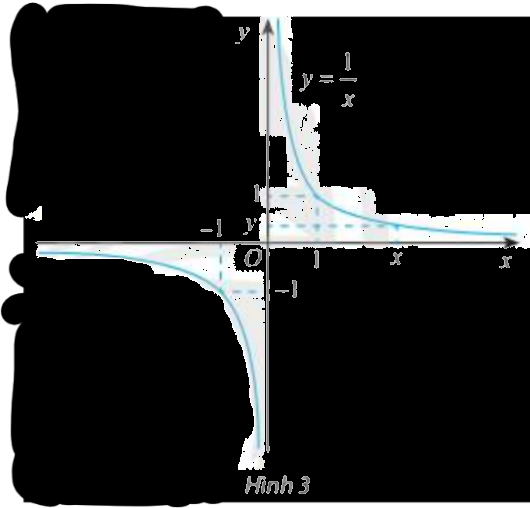
a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng lớn (dần tới \( + \infty \))?
b) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, nêu nhận xét về giá trị \(f\left( x \right)\) khi \(x\) càng bé (dần tới \( - \infty \))?
Phương pháp giải:
Để điền giá trị vào bảng, ta thay giá trị của \(x\) vào hàm số \(f\left( x \right) = \frac{1}{x}\).
Lời giải chi tiết:
a)
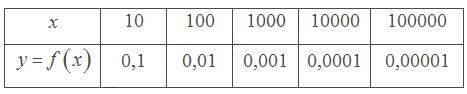
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
b)

Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}}\);
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}}\).
Phương pháp giải:
Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to + \infty } \frac{{1 - 3{x^2}}}{{{x^2} + 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}\left( {\frac{1}{{{x^2}}} - 3} \right)}}{{{x^2}\left( {1 + \frac{{2x}}{{{x^2}}}} \right)}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{{{x^2}}} - 3}}{{1 + \frac{2}{x}}} = \frac{{\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{x^2}}} - \mathop {\lim }\limits_{x \to + \infty } 3}}{{\mathop {\lim }\limits_{x \to + \infty } 1 + \mathop {\lim }\limits_{x \to + \infty } \frac{2}{x}}} = \frac{{0 - 3}}{{1 + 0}} = - 3\)
b) \(\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{2}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\mathop {\lim }\limits_{x \to - \infty } \frac{2}{{1 + \frac{1}{x}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}.\frac{{\mathop {\lim }\limits_{x \to - \infty } 2}}{{\mathop {\lim }\limits_{x \to - \infty } 1 + \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x}}} = 0.\frac{2}{{1 + 0}} = 0\).
Một cái hồ đang chứa \(200{m^3}\) nước mặn với nồng độ muối \(10kg/{m^3}\). Người ta ngọt hóa nước trong hồ bằng cách bơm nước ngọt vào hồ với tốc độ \(2{m^3}/\)phút.
a) Viết biểu thức \(C\left( t \right)\) biểu thị nồng độ muối trong hồ sau \(t\) phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right)\) và giải thích ý nghĩa.
Phương pháp giải:
a) Dựa vào dữ kiện của đề bài, biểu thị mối liên hệ giữa các đại lượng khối lượng muối, lượng nước trong hồ và nồng độ muối để viết biểu thức \(C\left( t \right)\).
b) Vận dụng phương pháp tính giới hạn của hàm số tại vô cực:
Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.
Lời giải chi tiết:
a) Khối lượng muối có trong hồ là: \(200.10 = 2000\left( {kg} \right)\).
Sau \(t\) phút kể từ khi bắt đầu bơm, lượng nước trong hồ là: \(200 + 2t\left( {{m^3}} \right)\).
Nồng độ muối tại thời điểm \(t\) phút kể từ khi bắt đầu bơm là: \(C\left( t \right) = \frac{{2000}}{{200 + 2t}}\left( {kg/{m^3}} \right)\)
b) \(\mathop {\lim }\limits_{t \to + \infty } C\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{200 + 2t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{t\left( {\frac{{200}}{t} + 2} \right)}} = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\mathop {\lim }\limits_{t \to + \infty } \frac{{2000}}{{\frac{{200}}{t} + 2}}\)
\( = \mathop {\lim }\limits_{t \to + \infty } \frac{1}{t}.\frac{{\mathop {\lim }\limits_{t \to + \infty } 2000}}{{\mathop {\lim }\limits_{t \to + \infty } \frac{{200}}{t} + \mathop {\lim }\limits_{t \to + \infty } 2}} = 0.\frac{{2000}}{{0 + 2}} = 0\)
Ý nghĩa: Khi \(t\) càng lớn thì nồng độ muối càng dần về 0, tức là đến một lúc nào đó nồng độ muối trong hồ không đáng kể, nước trong hồ gần như là nước ngọt.
Mục 4 của chương trình Toán 11 tập 1 Chân trời sáng tạo tập trung vào các kiến thức về vectơ trong không gian. Các bài tập trang 75 và 76 SGK yêu cầu học sinh vận dụng các định nghĩa, tính chất của vectơ, các phép toán vectơ (cộng, trừ, nhân với một số thực) và các ứng dụng của vectơ trong việc giải quyết các bài toán hình học không gian.
Bài tập này yêu cầu học sinh xác định vectơ chỉ phương và vectơ pháp tuyến của một đường thẳng cho trước. Để làm được điều này, học sinh cần nắm vững định nghĩa của vectơ chỉ phương và vectơ pháp tuyến, cũng như các phương pháp tìm vectơ trong không gian.
Ví dụ, cho đường thẳng d: x + 2y - z + 1 = 0. Vectơ pháp tuyến của đường thẳng d là n = (1, 2, -1).
Bài tập này yêu cầu học sinh xác định vị trí tương đối giữa hai đường thẳng: song song, cắt nhau hoặc chéo nhau. Để làm được điều này, học sinh cần sử dụng các điều kiện về vectơ chỉ phương và vectơ nối giữa hai điểm thuộc hai đường thẳng.
Ví dụ, xét hai đường thẳng d1 và d2. Nếu vectơ chỉ phương của d1 và d2 cùng phương và có một điểm thuộc d1 không thuộc d2 thì d1 và d2 song song.
Bài tập này yêu cầu học sinh tính góc giữa hai đường thẳng. Để làm được điều này, học sinh cần sử dụng công thức tính góc giữa hai vectơ và áp dụng vào trường hợp hai đường thẳng.
Công thức tính góc θ giữa hai vectơ a và b: cos(θ) = (a.b) / (||a||.||b||)
Bài tập này yêu cầu học sinh tính khoảng cách từ một điểm đến một đường thẳng. Để làm được điều này, học sinh cần sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng trong không gian.
Công thức tính khoảng cách d từ điểm M(x0, y0, z0) đến đường thẳng d: ax + by + cz + d = 0 là: d = |ax0 + by0 + cz0 + d| / √(a² + b² + c²)
Để giải các bài tập về vectơ trong không gian một cách hiệu quả, học sinh cần:
Học toán không chỉ là việc học thuộc công thức mà còn là việc hiểu bản chất của vấn đề. Hãy cố gắng suy nghĩ, phân tích và tìm tòi các phương pháp giải bài tập khác nhau. Đừng ngại hỏi thầy cô, bạn bè khi gặp khó khăn. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ |
| ||a|| = √(x² + y² + z²) | Độ dài của vectơ a |
| d = |ax0 + by0 + cz0 + d| / √(a² + b² + c²) | Khoảng cách từ điểm đến đường thẳng |