Chào mừng các em học sinh đến với lời giải chi tiết Bài 5 trang 49 SGK Toán 11 tập 2 - Chân trời sáng tạo. Bài học này thuộc chương trình học Toán 11, tập trung vào các kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
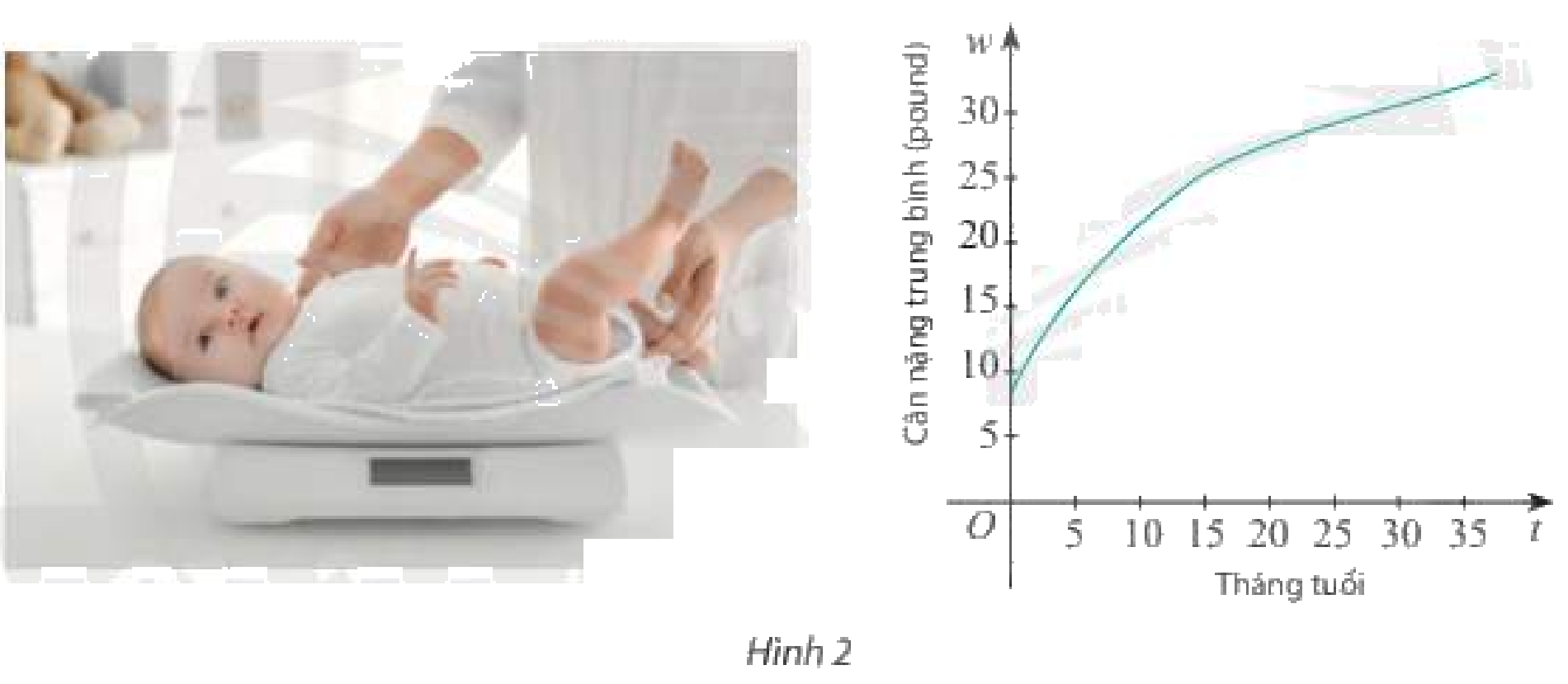
Cân nặng trung bình của một bé gái trong độ tuổi từ 0 đến 36 tháng có thể được tính gần đúng bởi hàm số (wleft( t right) = 0,000758{t^3} - 0,0596{t^2} + 1,82t + 8,15)
Đề bài
ân nặng trung bình của một bé gái trong độ tuổi từ 0 đến 36 tháng có thể được tính gần đúng bởi hàm số \(w\left( t \right) = 0,000758{t^3} - 0,0596{t^2} + 1,82t + 8,15\), trong đó \(t\) được tính bằng tháng và \(w\) được tính bằng pound (nguồn: https://www.cdc.gov/growthcharts/data/who/GrChrt_Boys). Tính tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi.
Phương pháp giải - Xem chi tiết
Tính \({\rm{w}}'\left( {10} \right)\).
Lời giải chi tiết
Ta có: \(w'\left( t \right) = 0,000758.3{t^2} - 0,0596.2t + 1,82.1 + 0 = 0,002274{t^2} - 0,1192t + 1,82\)
Tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi là:
\(w'\left( {10} \right) = 0,{002274.10^2} - 0,1192.10 + 1,82 = 0,8554\)
Bài 5 trang 49 SGK Toán 11 tập 2 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Bài tập này thường yêu cầu học sinh phải tính đạo hàm của hàm số, tìm cực trị của hàm số, hoặc giải các bài toán liên quan đến tối ưu hóa.
Bài 5 trang 49 SGK Toán 11 tập 2 - Chân trời sáng tạo thường bao gồm các dạng bài tập sau:
Để giải Bài 5 trang 49 SGK Toán 11 tập 2 - Chân trời sáng tạo một cách hiệu quả, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Dưới đây là lời giải chi tiết cho Bài 5 trang 49 SGK Toán 11 tập 2 - Chân trời sáng tạo:
Lời giải:
f'(x) = 3x2 + 4x - 5
Lời giải:
g'(x) = 2x - 4
Giải phương trình g'(x) = 0, ta được x = 2
Xét dấu g'(x), ta thấy g'(x) < 0 khi x < 2 và g'(x) > 0 khi x > 2. Do đó, hàm số g(x) đạt cực tiểu tại x = 2 và giá trị cực tiểu là g(2) = -1.
Để củng cố kiến thức và kỹ năng, học sinh có thể làm thêm các bài tập sau:
Bài 5 trang 49 SGK Toán 11 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu sâu hơn về đạo hàm và ứng dụng của nó. Bằng cách nắm vững các kiến thức và kỹ năng đã học, học sinh có thể giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả.
giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn này sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!