Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 Chân trời sáng tạo tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục 3 của chương trình Toán 11 tập 1 tập trung vào các kiến thức quan trọng về phép biến hình. Việc hiểu rõ và vận dụng thành thạo các kiến thức này là nền tảng cho các bài học tiếp theo.
Hoàn thành bảng giá trị sau đây:
Hoàn thành bảng giá trị sau đây:
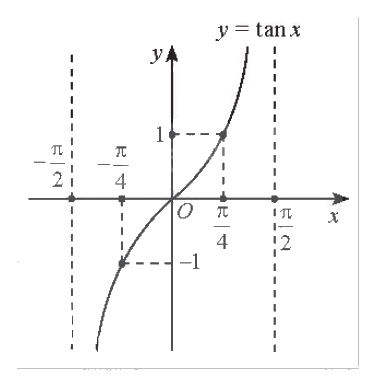
Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
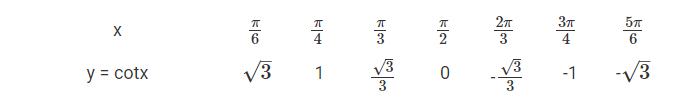
Hoàn thành bảng giá trị sau đây:

Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
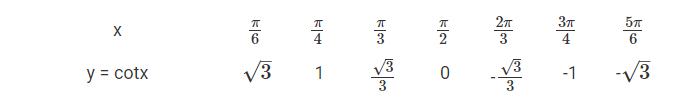
Li độ s (cm) của một con lắc đồng hộ theo thời gian t (giây) được cho bởi hàm số \(s = 2\cos \pi t\). Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 1 giây đầu thì li độ s nằm trong đoạn \(\left[ { - 1;1} \right]\,\,(cm)\).

Phương pháp giải:
Dựa vào đồ thị hàm côsin để giải quyết.
Lời giải chi tiết:
Ta có: \(s \in \left[ { - 1;1} \right]\, \Leftrightarrow - 1 \le 2\cos \pi t \le 1\)
\( \Leftrightarrow - \frac{1}{2} \le \cos \pi t \le \frac{1}{2}\)
Trong 1 giây đầu tiên \(0 < t < 1\) \( \Rightarrow 0 < \pi t < \pi \).
Đồ thị hàm số \(y = cosx\) trên \(\left[ {0;\pi } \right]\):
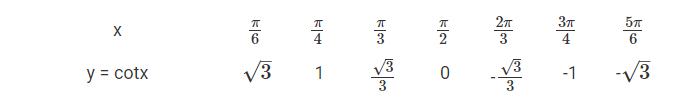
Dựa vào đồ thị ta thấy \( - \frac{1}{2} \le \cos \pi t \le \frac{1}{2} \Leftrightarrow \frac{\pi }{3} \le \pi t \le \frac{{2\pi }}{3} \Leftrightarrow \frac{1}{3} \le t \le \frac{2}{3}\)
Vậy \(t \in \left[ {\frac{1}{3};\frac{2}{3}} \right]\,\).
Hoàn thành bảng giá trị sau đây:

Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
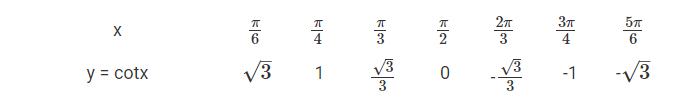
Hoàn thành bảng giá trị sau đây:

Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
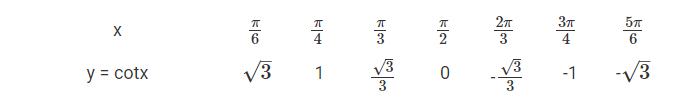
Có bao nhiêu giá trị x trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\) thỏa mãn điều kiện \(\tan x = 2\)?
Phương pháp giải:
Dựa vào đồ thị.
Lời giải chi tiết:

Từ đồ thị ta thấy có 4 giá trị x trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\) thỏa mãn điều kiện \(\tan x = 2\)
Cho hàm số \(y = \cos x\) với \(x \in \left[ { - \frac{\pi }{2};\pi } \right]\).
a) Vẽ đồ thị hàm số đã cho.
b) Tại các điểm nào thì giá trị hàm số lớn nhất?
c) Tìm các giá trị của x thuộc \(\left[ {\frac{{ - \pi }}{4};\frac{{5\pi }}{4}} \right]\) sao cho \(\sin \left( {x - \frac{\pi }{4}} \right) < 0\).
Lời giải chi tiết:
a) Ta có đồ thị hàm số \(y = \cos x\) với \(x \in \left[ { - \frac{\pi }{2};\pi } \right]\) như hình dưới:

b) Tại điểm x =0 thì giá trị hàm số lớn nhất.
c) Do \(x \in \left[ {\frac{{ - \pi }}{4};\frac{{5\pi }}{4}} \right]\) nên \(\left( {x - \frac{\pi }{4}} \right) \in \left[ {\frac{{ - \pi }}{2};\pi } \right]\).
Để \(\sin \left( {x - \frac{\pi }{4}} \right) < 0\) thì \(\left( {x - \frac{\pi }{4}} \right) \in \left[ {\frac{{ - \pi }}{2};0} \right]\).
Suy ra \(x \in \left[ {\frac{{ - \pi }}{4};\frac{\pi }{4}} \right]\).
Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong Hình 10. Trên bản đồ phẳng lấy đường xích đạo làm trục hoành và kinh tuyến \({0^o}\) làm trục tung. Khi đó tung độ của một điểm có vĩ độ \({\varphi ^o}\) \(( - {90^o} < \varphi < {90^o})\) được cho bởi hàm số \(y = 20\tan \left( {\frac{\pi }{{180}}\varphi } \right)\) (cm). Sử dụng đồ thị hàm số tang, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo 20cm trên bản đồ.
Phương pháp giải:
Vận dụng đồ thị của hàm số tan vào bài toán thực tế.
Lời giải chi tiết:
Ta có điểm nằm cách xích đạo 20cm có y = 20 hoặc y = - 20 nên \(\tan \left( {\frac{\pi }{{180}}\varphi } \right) = - 1\).
Vì \( - {90^o} < \varphi < {90^o}\) nên \( - \frac{\pi }{2} < \frac{\pi }{{180}}\varphi < \frac{\pi }{2}\).
Đặt \(x = \frac{\pi }{{180}}\varphi \) với \( - \frac{\pi }{2} < x < \frac{\pi }{2}\). Ta có đồ thị:

Từ đồ thị, ta có:
y = 1 khi \(x = \frac{\pi }{4} \Leftrightarrow \frac{\pi }{{180}}\varphi = \frac{\pi }{4} \Leftrightarrow \varphi = {45^o}\).
y = -1 khi \(x = - \frac{\pi }{4} \Leftrightarrow \frac{\pi }{{180}}\varphi = - \frac{\pi }{4} \Leftrightarrow \varphi = - {45^o}\).
Vậy trên bản đồ, các điểm nằm ở vĩ độ \({45^o}\) Bắc và \({45^o}\) Nam nằm cách xích đạo 20 cm.
Mục 3 trong SGK Toán 11 tập 1 Chân trời sáng tạo xoay quanh các kiến thức về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các tính chất và ứng dụng của các phép biến hình này là vô cùng quan trọng để giải quyết các bài toán hình học một cách hiệu quả.
Phép tịnh tiến là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ. Để thực hiện một phép tịnh tiến, ta cần xác định vectơ tịnh tiến. Vectơ tịnh tiến này sẽ chỉ ra hướng và độ dài của sự dịch chuyển.
Phép quay là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ và bảo toàn góc giữa hai đường thẳng bất kỳ. Để thực hiện một phép quay, ta cần xác định tâm quay và góc quay.
Phép đối xứng trục là phép biến hình biến mỗi điểm M thành điểm M’ sao cho đường thẳng nối M và M’ vuông góc với trục đối xứng và trung điểm của đoạn thẳng MM’ nằm trên trục đối xứng.
Phép đối xứng tâm là phép biến hình biến mỗi điểm M thành điểm M’ sao cho M và M’ đối xứng nhau qua tâm đối xứng.
Giải bài tập cụ thể:
Để giải các bài tập trong mục 3 trang 28, 29, 30, 31, 32 SGK Toán 11 tập 1 Chân trời sáng tạo, các em cần nắm vững định nghĩa, tính chất và ứng dụng của từng phép biến hình. Hãy bắt đầu bằng việc đọc kỹ đề bài, xác định các yếu tố quan trọng và lựa chọn phương pháp giải phù hợp. Đừng ngần ngại sử dụng các công cụ hỗ trợ như hình vẽ hoặc phần mềm hình học để minh họa và kiểm tra kết quả.
Lời khuyên:
Để học tốt môn Toán 11, các em cần dành thời gian ôn tập lý thuyết thường xuyên, làm nhiều bài tập thực hành và tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Nội dung |
|---|---|
| Bài 1 | Tìm ảnh của điểm M qua phép tịnh tiến Tv. |
| Bài 2 | Tìm ảnh của điểm M qua phép quay QO,α. |
| Bài 3 | Tìm ảnh của điểm M qua phép đối xứng trục Dd. |
| Bài 4 | Tìm ảnh của điểm M qua phép đối xứng tâm DI. |
Hy vọng với những kiến thức và hướng dẫn trên, các em sẽ tự tin giải quyết các bài tập trong mục 3 trang 28, 29, 30, 31, 32 SGK Toán 11 tập 1 Chân trời sáng tạo. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán nhé!