Bài 7 trang 50 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về các loại hàm số, tính đơn điệu, cực trị và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 7 trang 50, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
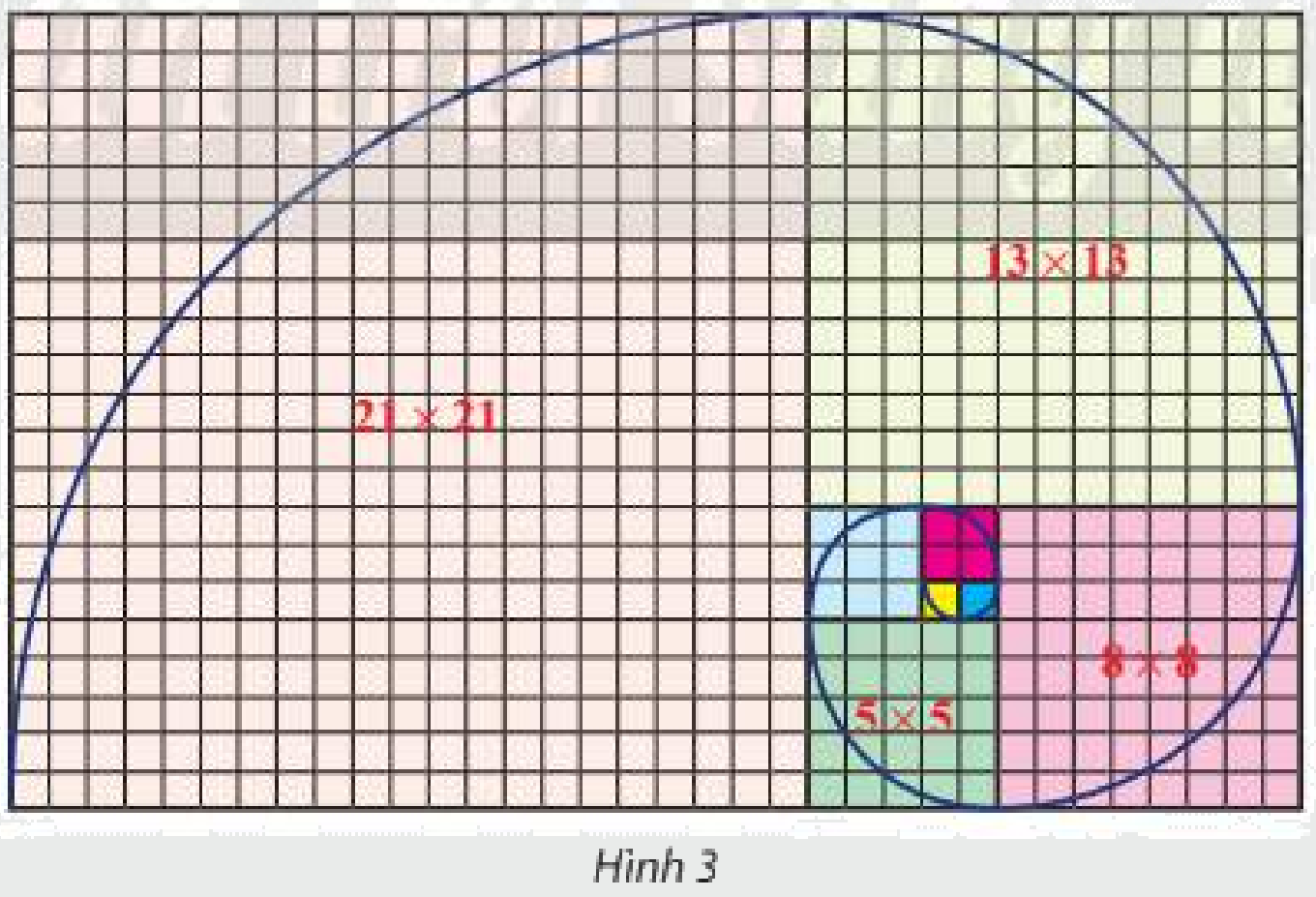
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đỏ từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
Đề bài
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đỏ từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
Phương pháp giải - Xem chi tiết
Dựa vào hình vẽ, tìm độ dài cạnh của các hình vuông theo thứ tự từ nhỏ đến lớn.
Lời giải chi tiết
Ta có: \({u_1} = 1;{u_2} = 1;{u_3} = 2;{u_4} = 3;{u_5} = 5;{u_6} = 8;{u_7} = 13;{u_8} = 21\)
Ta có:
\(\begin{array}{l}{u_3} = 2 = {u_2} + {u_1}\\{u_4} = 3 = {u_3} + {u_2}\\{u_5} = 5 = {u_4} + {u_3}\\{u_6} = 8 = {u_5} + {u_4}\\{u_7} = 13 = {u_6} + {u_5}\\{u_8} = 21 = {u_7} + {u_6}\end{array}\)
Ta thấy dãy số này kể từ số hạng thứ 3 bằng tổng của hai số hạng đứng trước nó.
Vậy dãy số này có công thức truy hồi là:
\(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + {u_{n - 2}}\left( {n \ge 3} \right)\end{array} \right.\)
Bài 7 trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số và ứng dụng của đạo hàm. Dưới đây là giải chi tiết bài tập này, cùng với hướng dẫn từng bước để bạn có thể tự giải và hiểu rõ hơn về phương pháp.
Bài 7 yêu cầu học sinh giải các bài toán liên quan đến việc xét tính đơn điệu của hàm số, tìm cực trị và vẽ đồ thị hàm số. Cụ thể, bài tập có thể bao gồm các dạng sau:
Để giải bài 7 trang 50, bạn cần nắm vững các kiến thức sau:
Ví dụ minh họa:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Để xét tính đơn điệu của hàm số, ta tính đạo hàm f'(x) = 3x2 - 6x. Giải phương trình f'(x) = 0, ta được x = 0 và x = 2. Lập bảng biến thiên, ta thấy hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.
Kiến thức về hàm số và ứng dụng của đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Để rèn luyện kỹ năng giải toán, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 11 tập 1 - Chân trời sáng tạo, hoặc tìm kiếm trên các trang web học toán online.
Bài 7 trang 50 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và ứng dụng của đạo hàm. Hy vọng với giải chi tiết và hướng dẫn trên, bạn đã hiểu rõ hơn về cách giải bài tập này và có thể tự giải các bài tập tương tự một cách hiệu quả.
| Khái niệm | Giải thích |
|---|---|
| Hàm số đơn điệu | Hàm số được gọi là đơn điệu trên một khoảng nếu nó luôn tăng hoặc luôn giảm trên khoảng đó. |
| Cực trị của hàm số | Điểm cực đại là điểm mà tại đó hàm số đạt giá trị lớn nhất trong một lân cận nào đó. Điểm cực tiểu là điểm mà tại đó hàm số đạt giá trị nhỏ nhất trong một lân cận nào đó. |