Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 28, 29, 30 sách giáo khoa Toán 11 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Nhắc lại rằng, độ pH của một dung dịch được tính theo công thức (pH = - log x), trong đó (x) là nồng độ ion H+ tính bằng mol/L.
Nhắc lại rằng, độ pH của một dung dịch được tính theo công thức \(pH = - \log x\), trong đó \(x\) là nồng độ ion H+ tính bằng mol/L.
Biết sữa có độ pH là 6,5. Nồng độ H+ của sữa bằng bao nhiêu?
Phương pháp giải:
Thay \(pH = 6,5\) vào công thức \(pH = - \log x\).
Lời giải chi tiết:
Ta có: \(pH = - \log x \Leftrightarrow 6,5 = - \log x \Leftrightarrow \log x = - 6,5 \Leftrightarrow x = {10^{ - 6,5}} \approx 3,{16.10^{ - 7}}\)
Vậy nồng độ H+ của sữa bằng \(3,{16.10^{ - 7}}\) mol/L.
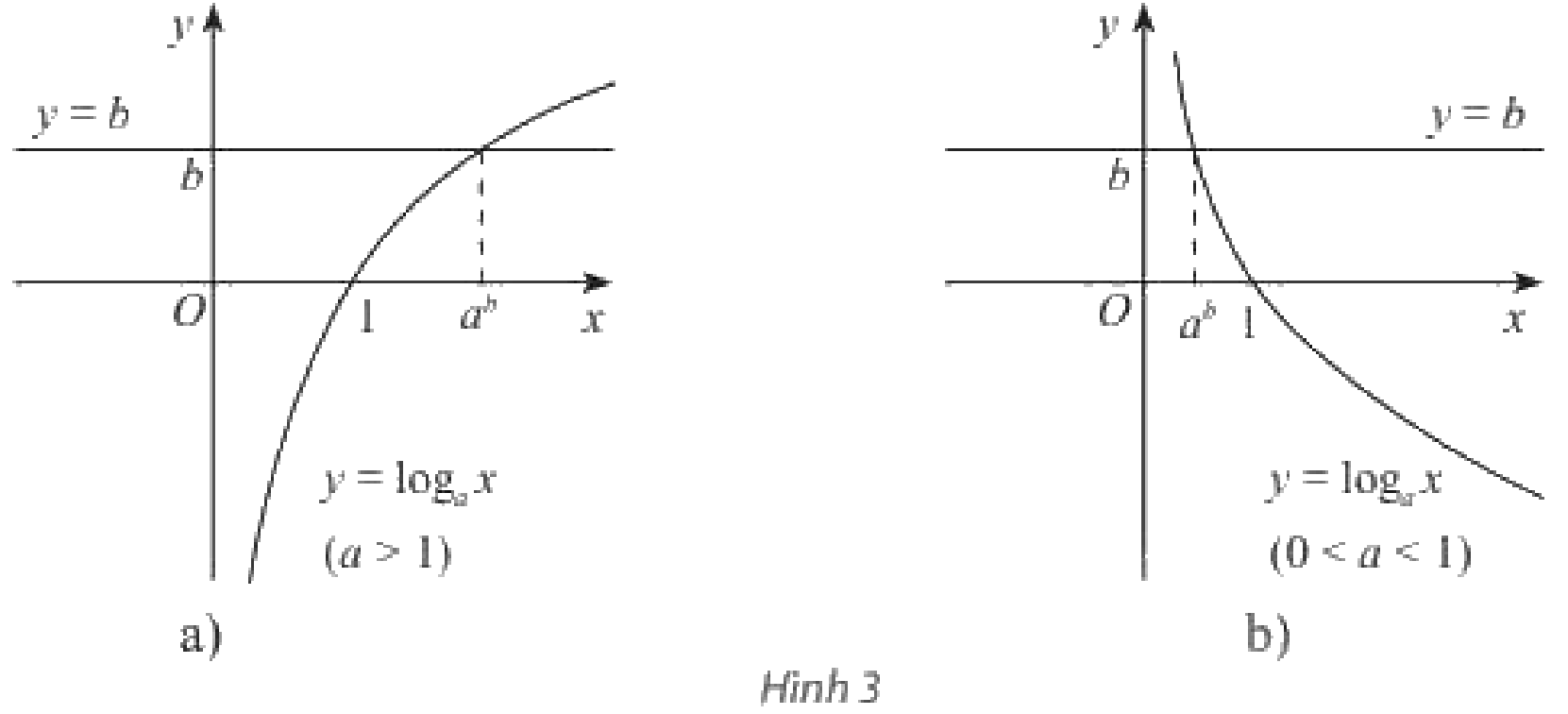
Cho đồ thị của hai hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) và \(y = b\) như Hình 3a (với \(a > 1\)) hay Hình 3b (với \(0 < a < 1\)). Từ đây hãy nhận xét về số nghiệm và công thức nghiệm của phương trình \({\log _a}x = b\).
Phương pháp giải:
Quan sát đồ thị, dựa vào số điểm chung của đồ thị của hai hàm số \(y = {\log _a}x\) và \(y = b\).
Lời giải chi tiết:
Đồ thị của hai hàm số \(y = {\log _a}x\) và \(y = b\) luôn cắt nhau tại một điểm duy nhất. Khi đó phương trình \({\log _a}x = b\) có nghiệm duy nhất \(x = {a^b}\).
Giải các phương trình sau:
a) \({\log _{\frac{1}{2}}}\left( {x - 2} \right) = - 2\);
b) \({\log _2}\left( {x + 6} \right) = {\log _2}\left( {x + 1} \right) + 1\)
Phương pháp giải:
Bước 1: Tìm ĐKXĐ.
Bước 2: Đưa 2 vế của phương trình về cùng cơ số và giải phương trình.
Bước 3: Kết luận.
Lời giải chi tiết:
a) \({\log _{\frac{1}{2}}}\left( {x - 2} \right) = - 2\)
Điều kiện: \(x - 2 > 0 \Leftrightarrow x > 2\)
\({\log _{\frac{1}{2}}}(x - 2) = - 2 \Leftrightarrow {\log _{\frac{1}{2}}}(x - 2) = {\log _{\frac{1}{2}}}{\left( {\frac{1}{2}} \right)^{ - 2}} \Leftrightarrow x - 2 = {\left( {\frac{1}{2}} \right)^{ - 2}} \Leftrightarrow x = 6\,\,(TMDK)\)
Vậy phương trình có nghiệm là \(x = 6\).
b) \({\log _2}\left( {x + 6} \right) = {\log _2}\left( {x + 1} \right) + 1\)
Điều kiện: \(\left\{ \begin{array}{l}x + 6 > 0\\x + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 6\\x > - 1\end{array} \right. \Leftrightarrow x > - 1\)
\(\begin{array}{l}{\log _2}(x + 6) = {\log _2}(x + 1) + 1 \Leftrightarrow {\log _2}(x + 6) = {\log _2}(x + 1) + {\log _2}2 = {\log _2}2(x + 1)\\ \Leftrightarrow x + 6 = 2(x + 1) \Leftrightarrow x = 4\,(TMDK)\end{array}\)
Vậy phương trình có nghiệm là \(x = 4\).
Mục 2 của SGK Toán 11 tập 2 - Chân trời sáng tạo tập trung vào các kiến thức về đạo hàm của hàm số. Cụ thể, các em sẽ được học về ý nghĩa của đạo hàm, quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của hàm hợp. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán liên quan đến đạo hàm trong chương trình Toán 11 và các chương trình nâng cao.
Đạo hàm của một hàm số tại một điểm biểu thị tốc độ thay đổi tức thời của hàm số tại điểm đó. Nói cách khác, đạo hàm cho ta biết hàm số tăng hay giảm như thế nào khi biến số độc lập thay đổi một lượng rất nhỏ. Ý nghĩa hình học của đạo hàm là hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm đó.
Để tính đạo hàm của các hàm số phức tạp, chúng ta sử dụng các quy tắc sau:
Bài 1 (Trang 28): Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1.
Lời giải:
f'(x) = (3x2)' + (2x)' - (1)' = 6x + 2 - 0 = 6x + 2.
Bài 2 (Trang 29): Tính đạo hàm của hàm số g(x) = (x2 + 1) / (x - 1).
Lời giải:
g'(x) = ((x2 + 1)'(x - 1) - (x2 + 1)(x - 1)') / (x - 1)2 = (2x(x - 1) - (x2 + 1)) / (x - 1)2 = (2x2 - 2x - x2 - 1) / (x - 1)2 = (x2 - 2x - 1) / (x - 1)2.
Bài 3 (Trang 30): Tính đạo hàm của hàm số h(x) = sin(2x).
Lời giải:
h'(x) = cos(2x) * (2x)' = 2cos(2x).
Để hiểu sâu hơn về đạo hàm, các em nên tự mình giải thêm nhiều bài tập khác nhau. Các em có thể tìm thấy các bài tập tương tự trong sách bài tập Toán 11 tập 2 hoặc trên các trang web học toán online. Ngoài ra, việc vẽ đồ thị hàm số và so sánh với đạo hàm cũng giúp các em hiểu rõ hơn về mối liên hệ giữa đạo hàm và tính chất của hàm số.
Hy vọng với những hướng dẫn chi tiết trên, các em sẽ tự tin hơn khi giải các bài tập về đạo hàm trong SGK Toán 11 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!