Bài 1 trang 56 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc rèn luyện kỹ năng giải bài toán về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm giới hạn của hàm số tại một điểm cho trước.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 1 trang 56 SGK Toán 11 tập 2, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp (S.ABCD) có đáy là hình thoi (ABCD) cạnh (a). Cho biết (SA = asqrt 3 ,SA bot AB) và (SA bot A{rm{D}}).
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 ,SA \bot AB\) và \(SA \bot A{\rm{D}}\). Tính góc giữa \(SB\) và \(C{\rm{D}}\), \(S{\rm{D}}\) và \(C{\rm{B}}\).
Phương pháp giải - Xem chi tiết
Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).
Lời giải chi tiết
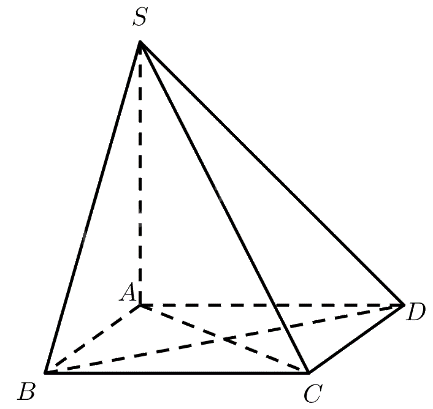
a) Ta có: \(C{\rm{D}}\parallel AB \Rightarrow \left( {SB,C{\rm{D}}} \right) = \left( {SB,AB} \right) = \widehat {SBA}\).
\(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SBA} = {60^ \circ }\)
Vậy \(\left( {SB,C{\rm{D}}} \right) = {60^ \circ }\).
a) Ta có: \(C{\rm{B}}\parallel AD \Rightarrow \left( {SD,C{\rm{B}}} \right) = \left( {SD,AD} \right) = \widehat {S{\rm{D}}A}\).
\(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SDA} = {60^ \circ }\)
Vậy \(\left( {SD,C{\rm{B}}} \right) = {60^ \circ }\).
Bài 1 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về giới hạn hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 1 yêu cầu tính các giới hạn sau:
1. limx→2 (x2 - 3x + 2) / (x - 2)
Ta có thể phân tích tử thức thành (x - 1)(x - 2). Do đó:
limx→2 (x2 - 3x + 2) / (x - 2) = limx→2 (x - 1)(x - 2) / (x - 2) = limx→2 (x - 1) = 2 - 1 = 1
2. limx→-1 (x3 + 1) / (x + 1)
Ta có thể phân tích tử thức thành (x + 1)(x2 - x + 1). Do đó:
limx→-1 (x3 + 1) / (x + 1) = limx→-1 (x + 1)(x2 - x + 1) / (x + 1) = limx→-1 (x2 - x + 1) = (-1)2 - (-1) + 1 = 1 + 1 + 1 = 3
3. limx→0 (sin x) / x
Đây là một giới hạn lượng giác cơ bản. Sử dụng định lý giới hạn đặc biệt, ta có:
limx→0 (sin x) / x = 1
4. limx→1 (x2 - 1) / (x - 1)
Ta có thể phân tích tử thức thành (x - 1)(x + 1). Do đó:
limx→1 (x2 - 1) / (x - 1) = limx→1 (x - 1)(x + 1) / (x - 1) = limx→1 (x + 1) = 1 + 1 = 2
Để giải các bài tập về giới hạn hàm số, bạn cần nắm vững các kiến thức sau:
Khi gặp một bài tập về giới hạn, bạn nên:
Bài tập: Tính limx→3 (x2 - 9) / (x - 3)
Lời giải:
limx→3 (x2 - 9) / (x - 3) = limx→3 (x - 3)(x + 3) / (x - 3) = limx→3 (x + 3) = 3 + 3 = 6
Hy vọng với lời giải chi tiết và hướng dẫn trên, bạn đã hiểu rõ cách giải Bài 1 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo. Chúc bạn học tốt!