Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 116, 117 SGK Toán 11 tập 1 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 11.
Bài tập trong mục này tập trung vào các kiến thức về...
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
Cho ba mặt phẳng song song \(\left( P \right),\left( Q \right),\left( R \right)\) lần lượt cắt hai đường thăng \(a\) và \(a'\) tại các điểm \(A,B,C\) và \(A',B',C'\). Gọi \({B_1}\) là giao điểm của \(AC'\) với \(\left( Q \right)\) (Hình 12).
a) Trong tam giác \(ACC'\), có nhận xét gì về mối liên hệ giữa \(\frac{{AB}}{{BC}}\) và \(\frac{{A{B_1}}}{{{B_1}C'}}\)?
b) Trong tam giác \(AA'C'\), có nhận xét gì về mối liên hệ giữa \(\frac{{A{B_1}}}{{{B_1}C'}}\) và \(\frac{{A'B'}}{{B'C'}}\)?
c) Từ đó, nếu nhận xét về mối liên hệ giữa các tỉ số \(\frac{{AB}}{{A'B'}},\frac{{BC}}{{B'C'}},\frac{{AC}}{{A'C'}}\).
Phương pháp giải:
‒ Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.
‒ Sử dụng định lí Thalès trong tam giác.
‒ Sử dụng tính chất của tỉ lệ thức.
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( {ACC'} \right) \cap \left( Q \right) = B{B_1}\\\left( {ACC'} \right) \cap \left( R \right) = CC'\end{array} \right\} \Rightarrow B{B_1}\parallel CC' \Rightarrow \frac{{AB}}{{BC}} = \frac{{A{B_1}}}{{{B_1}C'}}\left( 1 \right)\)
b) Ta có:
\(\left. \begin{array}{l}\left( P \right)\parallel \left( Q \right)\\\left( {AA'C'} \right) \cap \left( Q \right) = B{B_1}\\\left( {AA'C'} \right) \cap \left( P \right) = AA'\end{array} \right\} \Rightarrow B{B_1}\parallel AA' \Rightarrow \frac{{A{B_1}}}{{{B_1}C'}} = \frac{{A'B'}}{{B'C'}}\left( 2 \right)\)
c) Từ (1) và (2) suy ra \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AB + BC}}{{A'B' + B'C'}} = \frac{{AC}}{{A'C'}}\)
Vậy \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\).
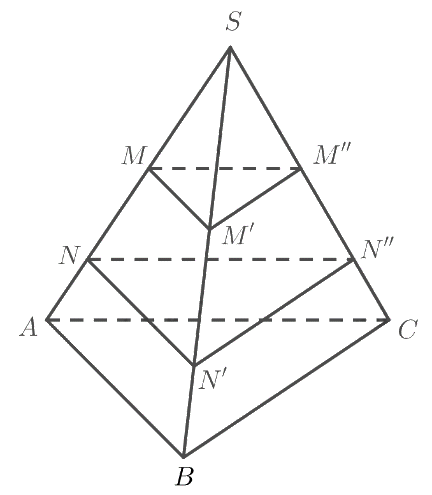
Cho hình chóp \(S.ABC\) có \(SA = 9,SB = 12,SC = 15\). Trên cạnh \(SA\) lấy các điểm \(M,N\) sao cho \(SM = 4,MN = 3,N4 = 2\). Vẽ hai mặt phẳng song song với mặt phẳng \(\left( {ABC} \right)\), lần lượt đi qua \(M,N\), cắt \(SB\) theo thứ tự tại \(M',N'\) và cắt \(SC\) theo thứ tự tại \(M'',N''\). Tính độ dài các đoạn thẳng \(SM',M'N',{\rm{ }}M''N'',N''C\).
Phương pháp giải:
Sử dụng định lí Thalès trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:

Ta có: \(\left( {MM'M''} \right)\parallel \left( {NN'N''} \right)\parallel \left( {ABC} \right)\) nên theo định lí Thalès ta có:
\(\frac{{SM}}{{SA}} = \frac{{SM'}}{{SB}} \Leftrightarrow SM' = \frac{{SM.SB}}{{SA}} = \frac{{4.12}}{9} = \frac{{16}}{3}\)
\(\frac{{SA}}{{SB}} = \frac{{MN}}{{M'N'}} \Leftrightarrow M'N' = \frac{{MN.SB}}{{SA}} = \frac{{3.12}}{9} = 4\)
\(\frac{{SA}}{{SC}} = \frac{{MN}}{{M''N''}} \Leftrightarrow M''N'' = \frac{{MN.SC}}{{SA}} = \frac{{3.15}}{9} = 5\)
\(\frac{{SA}}{{SC}} = \frac{{NA}}{{N''C}} \Leftrightarrow N''C = \frac{{NA.SC}}{{SA}} = \frac{{2.15}}{9} = \frac{{10}}{3}\)
Mục 4 của SGK Toán 11 tập 1 - Chân trời sáng tạo thường xoay quanh các chủ đề về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học phức tạp hơn trong chương trình học.
Phép tịnh tiến là một phép biến hình quan trọng trong hình học, giúp di chuyển một đối tượng hình học mà không làm thay đổi kích thước và hình dạng của nó. Để giải các bài toán liên quan đến phép tịnh tiến, cần hiểu rõ định nghĩa, tính chất và cách xác định ảnh của một điểm hoặc một hình qua phép tịnh tiến.
Phép quay là một phép biến hình khác, xoay một đối tượng hình học quanh một điểm cố định (gọi là tâm quay) một góc cho trước. Việc hiểu rõ các yếu tố của phép quay (tâm quay, góc quay, chiều quay) là rất quan trọng để giải các bài toán liên quan.
Phép đối xứng trục là phép biến hình biến mỗi điểm M thành điểm M' sao cho M' nằm trên đường thẳng d (trục đối xứng) và d là đường trung trực của đoạn thẳng MM'.
Để giải các bài toán về phép đối xứng trục, cần xác định đúng trục đối xứng và tìm điểm đối xứng của mỗi điểm qua trục đó.
Phép đối xứng tâm là phép biến hình biến mỗi điểm M thành điểm M' sao cho I là trung điểm của đoạn thẳng MM' (với I là tâm đối xứng).
Tương tự như phép đối xứng trục, việc xác định đúng tâm đối xứng là yếu tố then chốt để giải quyết các bài toán liên quan.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 4 trang 116, 117 SGK Toán 11 tập 1 - Chân trời sáng tạo:
(Giải thích chi tiết từng bước giải bài tập 1, kèm theo hình vẽ minh họa nếu cần thiết)
(Giải thích chi tiết từng bước giải bài tập 2, kèm theo hình vẽ minh họa nếu cần thiết)
(Giải thích chi tiết từng bước giải bài tập 3, kèm theo hình vẽ minh họa nếu cần thiết)
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh đã hiểu rõ hơn về các kiến thức về phép biến hình và có thể tự tin giải các bài tập tương tự. Chúc các em học tập tốt!