Chào mừng các em học sinh đến với lời giải chi tiết Bài 4 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo. Bài học này thuộc chương trình học Toán 11, tập trung vào các kiến thức về phép biến hình.
giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Vẽ đồ thị các hàm số:
Đề bài
Vẽ đồ thị các hàm số:
a) \(y = \log x\);
b) \(y = {\log _{\frac{1}{4}}}x\).
Phương pháp giải - Xem chi tiết
Lập bảng giá trị, dựa vào bảng giá trị vẽ đồ thị.
Lời giải chi tiết
a) Bảng giá trị:
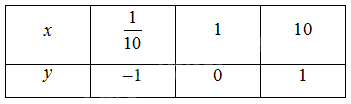
Đồ thị:
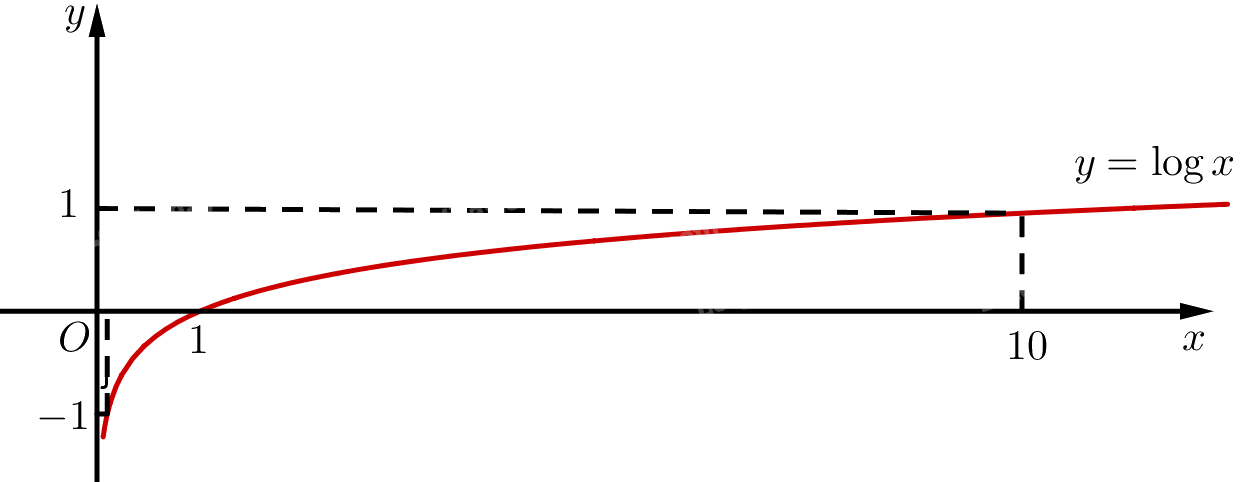
b) Bảng giá trị:
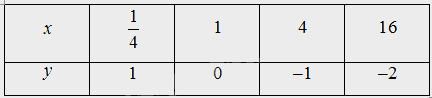
Đồ thị:
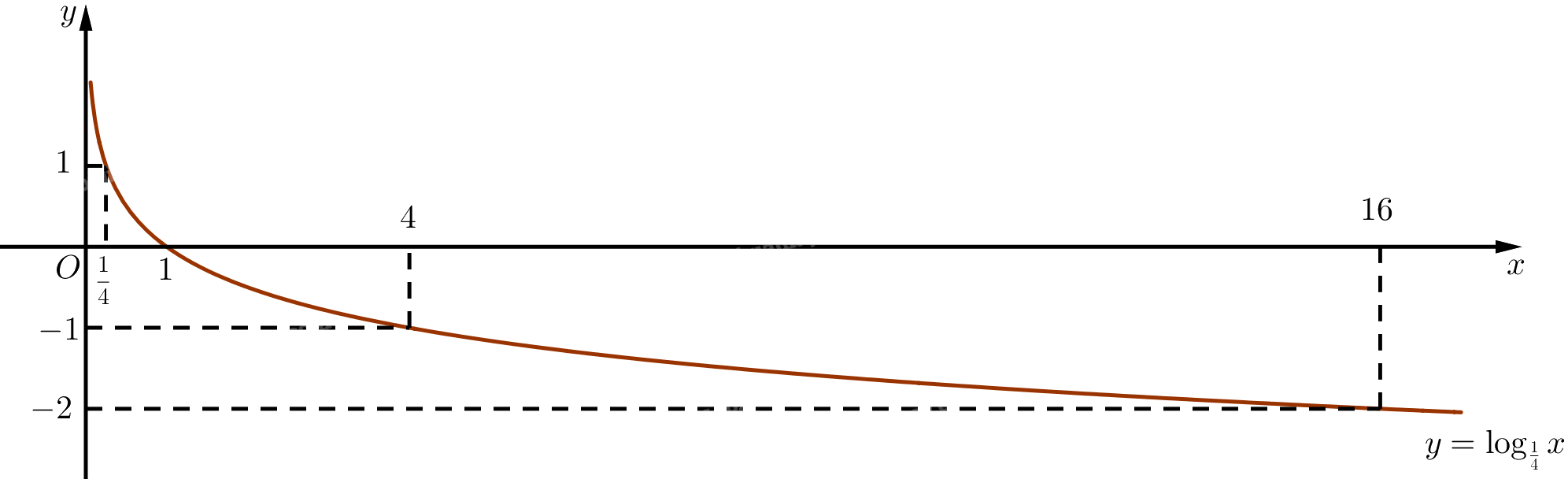
Bài 4 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về phép biến hình, cụ thể là phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết từng phần của bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Đề bài: Cho điểm A(1; 2). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến theo vectơ v = (3; -1).
Lời giải:
Công thức phép tịnh tiến: A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b)
Áp dụng công thức, ta có:
A'(1 + 3; 2 - 1) = A'(4; 1)
Vậy, tọa độ điểm A' là (4; 1).
Đề bài: Cho điểm B(-2; 3). Tìm tọa độ điểm B' là ảnh của B qua phép quay tâm O(0; 0) góc 90o.
Lời giải:
Công thức phép quay tâm O(0; 0) góc α:
B'(x' ; y') = B(x; y) * R(α) = (x*cos(α) - y*sin(α); x*sin(α) + y*cos(α))
Với α = 90o, ta có cos(90o) = 0 và sin(90o) = 1.
Áp dụng công thức, ta có:
B'(-2*0 - 3*1; -2*1 + 3*0) = B'(-3; -2)
Vậy, tọa độ điểm B' là (-3; -2).
Đề bài: Cho điểm C(4; -1). Tìm tọa độ điểm C' là ảnh của C qua phép đối xứng trục Ox.
Lời giải:
Công thức phép đối xứng trục Ox: C'(x'; y') = C(x; y) = (x; -y)
Áp dụng công thức, ta có:
C'(4; -(-1)) = C'(4; 1)
Vậy, tọa độ điểm C' là (4; 1).
Đề bài: Cho điểm D(-1; 5). Tìm tọa độ điểm D' là ảnh của D qua phép đối xứng tâm I(2; -3).
Lời giải:
Công thức phép đối xứng tâm I(a; b): D'(x'; y') = D(x; y) = (2a - x; 2b - y)
Áp dụng công thức, ta có:
D'(2*2 - (-1); 2*(-3) - 5) = D'(5; -11)
Vậy, tọa độ điểm D' là (5; -11).
Để củng cố kiến thức về phép biến hình, các em có thể tự giải thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và áp dụng thành thạo vào giải các bài toán phức tạp hơn.
Hy vọng với lời giải chi tiết Bài 4 trang 25 SGK Toán 11 tập 2 - Chân trời sáng tạo này, các em học sinh đã hiểu rõ cách áp dụng các phép biến hình để giải quyết các bài toán cụ thể. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!