Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 121 và 122 sách giáo khoa Toán 11 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Trong hoạt động mở đầu:
Trong hoạt động mở đầu:
a) Các tia sáng \(AA',BB',DD'\) có song song với nhau hay không?
b) Nêu cách xác định bóng \(C'\) của điểm \(C\) trên mặt đường.
Phương pháp giải:
‒ Sử dụng định lí: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Lời giải chi tiết:
a) \(AA'\parallel BB'\parallel DD'\) vì cùng song song với đường thẳng \(l\).
b) Cách xác định bóng \(C'\) của điểm \(C\) trên mặt đường:
‒ Qua \(C\) dựng đường thẳng \(d\) song song với đường thẳng \(l\).
‒ Giao điểm của đường thẳng \(d\) với mặt đường chính là bóng \(C'\) của điểm \(C\).
Tìm phương chiếu, mặt phẳng chiếu của phép chiếu song song được mô tả trong Hình 2.
Phương pháp giải:
Sử dụng định nghĩa phép chiếu song song.
Lời giải chi tiết:
Phương chiếu: đường thẳng \(a\).
Mặt phẳng chiếu: Mặt phẳng \(\left( Q \right)\).
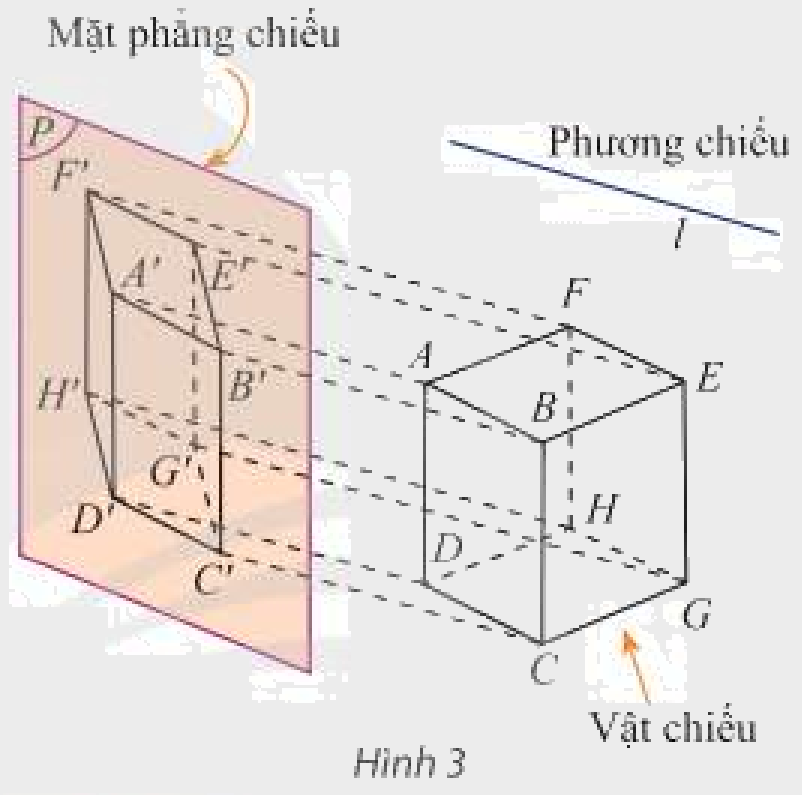
Tìm ảnh của hình hộp \(ABEF.DCGH\) qua phép chiếu song song được mô tả trong Hình 3.

Phương pháp giải:
Sử dụng định nghĩa phép chiếu song song.
Lời giải chi tiết:
Ảnh của hình hộp \(ABEF.DCGH\) qua phép chiếu song song được mô tả trong Hình 3 là hình \(A'B'E'F'.D'C'G'H'\)
Mục 1 của chương trình Toán 11 tập 1, Chân trời sáng tạo, thường tập trung vào các khái niệm cơ bản về hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng. Việc nắm vững kiến thức trong mục này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong các chương tiếp theo.
Bài tập này yêu cầu học sinh xác định các hệ số a, b, c trong hàm số bậc hai cho trước. Để giải bài tập này, các em cần nắm vững định nghĩa hàm số bậc hai và khả năng nhận biết các hệ số.
Ví dụ: Cho hàm số y = 2x2 - 5x + 1. Xác định a, b, c.
Lời giải: a = 2, b = -5, c = 1.
Bài tập này yêu cầu học sinh tìm tọa độ đỉnh của parabol, tức là điểm cực trị của hàm số bậc hai. Để giải bài tập này, các em cần sử dụng công thức x = -b/2a để tìm hoành độ đỉnh, sau đó thay giá trị x vào hàm số để tìm tung độ đỉnh.
Ví dụ: Tìm tọa độ đỉnh của parabol y = x2 - 4x + 3.
Lời giải: x = -(-4)/(2*1) = 2. y = 22 - 4*2 + 3 = -1. Vậy tọa độ đỉnh là (2, -1).
Bài tập này yêu cầu học sinh vẽ đồ thị hàm số bậc hai. Để vẽ đồ thị, các em cần xác định các yếu tố quan trọng như tọa độ đỉnh, trục đối xứng, giao điểm với trục tung và trục hoành (nếu có).
Các bước vẽ đồ thị:
Để giải nhanh các bài tập về hàm số bậc hai, các em có thể áp dụng một số mẹo sau:
Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 121, 122 SGK Toán 11 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!