Bài 3 trang 126 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc giải quyết các bài toán liên quan đến phép biến hình. Bài tập này giúp học sinh củng cố kiến thức về các phép biến hình cơ bản và ứng dụng chúng vào giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 3 trang 126, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Vẽ hình biểu diễn của một hình vuông nội tiếp trong một hình tròn.
Đề bài
Vẽ hình biểu diễn của một hình vuông nội tiếp trong một hình tròn.
Phương pháp giải - Xem chi tiết
Sử dụng các quy tắc vẽ hình biểu diễn và tính chất của lục giác đều.
Lời giải chi tiết
Hình biểu diễn của hình vuông là hình bình hành, hình biểu diễn của hình tròn là hình elip. Vậy ta có hình biểu diễn như sau:
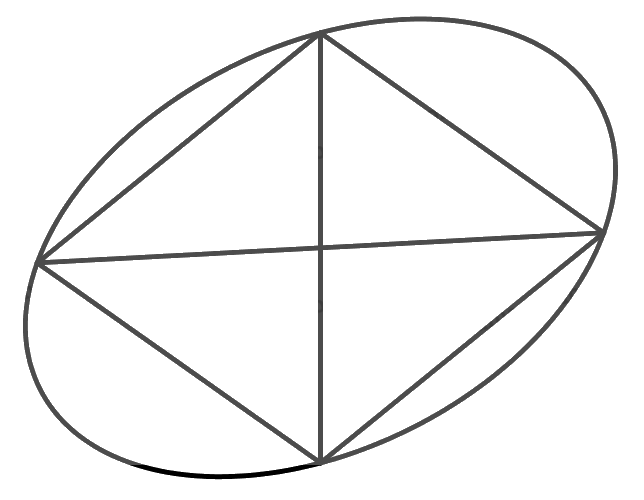
Bài 3 trang 126 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, yêu cầu học sinh vận dụng kiến thức về phép biến hình để giải quyết các vấn đề cụ thể. Dưới đây là giải chi tiết bài tập này, cùng với hướng dẫn từng bước để giúp các em hiểu rõ hơn về phương pháp giải.
Bài 3 yêu cầu học sinh thực hiện các phép biến hình (tịnh tiến, quay, đối xứng trục, đối xứng tâm) lên một hình cho trước và xác định ảnh của hình đó sau phép biến hình. Bài tập thường bao gồm các yêu cầu sau:
Để giải Bài 3 trang 126, các em cần nắm vững các kiến thức sau:
Ví dụ minh họa:
Giả sử cho điểm A(x0, y0) và phép tịnh tiến theo vector v = (a, b). Ảnh của điểm A qua phép tịnh tiến là điểm A'(x0 + a, y0 + b).
Tương tự, cho đường thẳng d: ax + by + c = 0 và phép tịnh tiến theo vector v = (a, b). Ảnh của đường thẳng d qua phép tịnh tiến là đường thẳng d': ax + by + c - a(x0 + a) - b(y0 + b) = 0.
Để giải các bài tập tương tự Bài 3 trang 126, các em có thể áp dụng các bước sau:
Khi giải các bài tập về phép biến hình, các em cần chú ý đến các điểm sau:
Bài 3 trang 126 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp các em củng cố kiến thức về phép biến hình và rèn luyện kỹ năng giải toán. Hy vọng với giải chi tiết và hướng dẫn trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!