Chào mừng bạn đến với bài học về Lý thuyết Phép tính Lôgarit trong chương trình Toán 11 Chân trời sáng tạo tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan và chi tiết về các khái niệm, tính chất và ứng dụng của phép tính lôgarit.
Chúng tôi cam kết mang đến cho bạn những kiến thức toán học chính xác, dễ hiểu và được trình bày một cách logic, giúp bạn tự tin hơn trong quá trình học tập và giải quyết các bài toán liên quan.
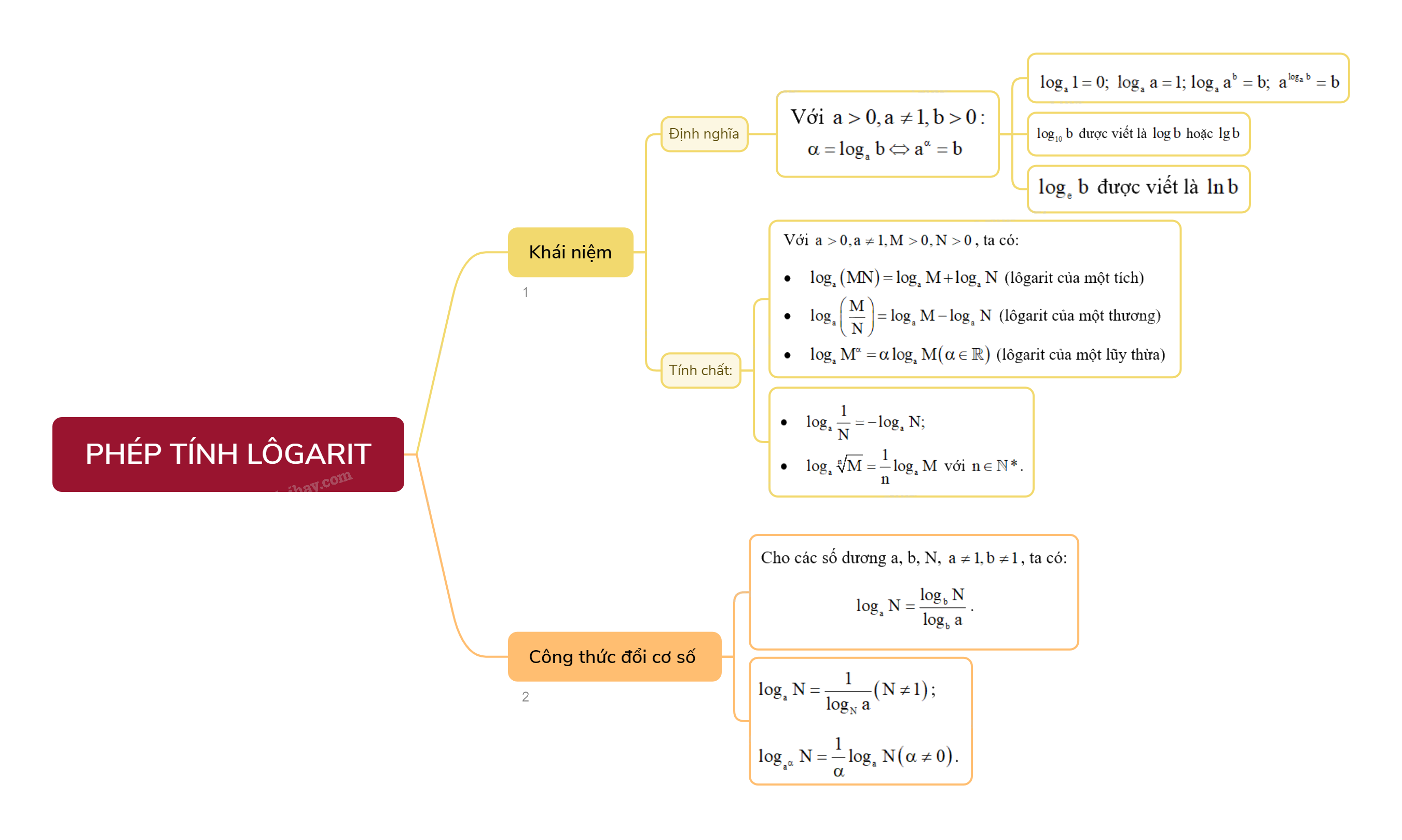
1. Khái niệm lôgarit Cho hai số thực dương a, b với \(a \ne 1\). Số thực \(\alpha \) thỏa mãn đẳng thức \({a^\alpha } = b\) được gọi là lôgarit cơ số a của b và kí hiệu là \({\log _a}b\).
1. Khái niệm lôgarit
Cho hai số thực dương a, b với \(a \ne 1\). Số thực \(\alpha \) thỏa mãn đẳng thức \({a^\alpha } = b\) được gọi là lôgarit cơ số a của b và kí hiệu là \({\log _a}b\).
\(\alpha = {\log _a}b \Leftrightarrow {a^\alpha } = b\).
Chú ý:
Từ định nghĩa, ta có:
2. Tính chất
Với \(a > 0,a \ne 1,M > 0,N > 0\), ta có:
Chú ý: Đặc biệt, ta có:
3. Công thức đổi cơ số
Cho các số dương a, b, N, \(a \ne 1,b \ne 1\), ta có:
\({\log _a}N = \frac{{{{\log }_b}N}}{{{{\log }_b}a}}\).
Đặc biệt, ta có:
\({\log _a}N = \frac{1}{{{{\log }_N}a}}\left( {N \ne 1} \right)\); \({\log _{{a^\alpha }}}N = \frac{1}{\alpha }{\log _a}N\left( {\alpha \ne 0} \right)\).
Phép tính lôgarit là một trong những khái niệm quan trọng trong chương trình Toán 11, đặc biệt là trong chương trình Chân trời sáng tạo. Nó đóng vai trò nền tảng cho nhiều lĩnh vực khác nhau của toán học và khoa học tự nhiên. Bài viết này sẽ trình bày chi tiết về lý thuyết phép tính lôgarit, bao gồm định nghĩa, tính chất, các dạng bài tập thường gặp và phương pháp giải.
Lôgarit của một số dương b theo cơ số a (với a > 0 và a ≠ 1) là số x sao cho ax = b. Ký hiệu: logab = x.
Dưới đây là một số tính chất cơ bản của lôgarit mà bạn cần nắm vững:
Có hai loại lôgarit thường được sử dụng:
Hàm số y = logax (với a > 0 và a ≠ 1) được gọi là hàm lôgarit. Hàm số này có những đặc điểm sau:
Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức lôgarit. Để giải phương trình lôgarit, ta thường sử dụng các tính chất của lôgarit để đưa phương trình về dạng đơn giản hơn.
Ví dụ: Giải phương trình log2(x + 1) = 3
Ta có: x + 1 = 23 = 8
Suy ra: x = 7
Bất phương trình lôgarit là bất phương trình có chứa ẩn số trong biểu thức lôgarit. Khi giải bất phương trình lôgarit, cần chú ý đến điều kiện xác định của lôgarit và xét dấu của cơ số.
Ví dụ: Giải bất phương trình log0.5(x - 2) > 1
Vì cơ số 0.5 < 1, ta đổi chiều bất đẳng thức khi bỏ lôgarit:
x - 2 < (0.5)1 = 0.5
Suy ra: x < 2.5
Kết hợp với điều kiện xác định x - 2 > 0, ta có: 2 < x < 2.5
Phép tính lôgarit có nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Phép tính Lôgarit - Toán 11 Chân trời sáng tạo. Chúc bạn học tập tốt!