Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 64 và 65 sách giáo khoa Toán 11 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Cho dãy số (left( {{u_n}} right)) với .({u_n} = frac{{{{left( { - 1} right)}^n}}}{n}).
Cho dãy số \(\left( {{u_n}} \right)\) với .\({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\).
a) Tìm các giá trị còn thiếu trong bảng sau:
b) Với \(n\) thế nào thì \(\left| {{u_n}} \right|\) bé hơn 0,01; 0,001?
c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.

Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm \({u_n}\) đến điểm 0 khi \(n\) trở nên rất lớn?
Phương pháp giải:
a) Để tìm \(\left| {{u_n}} \right|\), ta thay \(n\) vào công thức \(\left| {{u_n}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right|\).
b) Để tìm \(n\), ta giải các bất đẳng thức \(\left| {{u_n}} \right| < 0,01;\left| {{u_n}} \right| < 0,001\).
Lời giải chi tiết:
a) \(n = 100 \Leftrightarrow \left| {{u_{100}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{100}}}}{{100}}} \right| = \frac{1}{{100}} = 0,01\)
\(n = 1000 \Leftrightarrow \left| {{u_{1000}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{1000}}}}{{1000}}} \right| = \frac{1}{{1000}} = 0,001\)
Như vậy ta có thể điền vào bảng như sau:

b) \(\left| {{u_n}} \right| < 0,01 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,01 \Leftrightarrow \frac{1}{n} < 0,01 \Leftrightarrow n > 100\)
Vậy \(\left| {{u_n}} \right| < 0,01\) khi \(n > 100\).
\(\left| {{u_n}} \right| < 0,001 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,001 \Leftrightarrow \frac{1}{n} < 0,001 \Leftrightarrow n > 1000\)
Vậy \(\left| {{u_n}} \right| < 0,001\) khi \(n > 1000\).
c) Dựa vào trục số ta thấy, khoảng cách từ điểm \({u_n}\) đến điểm 0 trở nên rất bé khi \(n\) trở nên rất lớn.
Tính các giới hạn sau:
a) \(\lim \frac{1}{{{n^2}}}\);
b) \(\lim {\left( { - \frac{3}{4}} \right)^n}\).
Phương pháp giải:
Áp dụng giới hạn cơ bản:
• \(\lim \frac{1}{{{n^k}}} = 0\), với \(k\) nguyên dương bất kì.
• \(\lim {q^n} = 0\), với \(q\) là số thực thỏa mãn \(\left| q \right| < 1\).
Lời giải chi tiết:
a) Áp dụng công thức giới hạn cơ bản với \(k = 2\), ta có: \(\lim \frac{1}{{{n^2}}}\).
b) Do \(\left| { - \frac{3}{4}} \right| = \frac{3}{4} < 1\) nên \(\lim {\left( { - \frac{3}{4}} \right)^n} = 0\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{2n + 1}}{n}\).
a) Cho dãy số \(\left( {{v_n}} \right)\) với \({v_n} = {u_n} - 2\). Tìm giới hạn \(\lim {v_n}\).
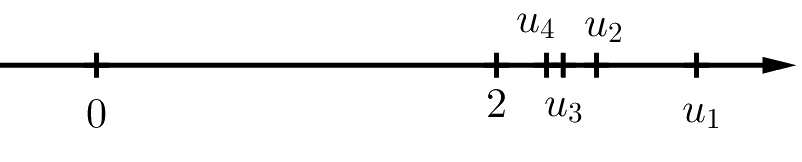
b) Biểu diễn các điểm \({u_1},{u_2},{u_3},{u_4}\) trên trục số. Có nhận xét gì về vị trí của các điểm \({u_n}\) khi \(n\) trở nên rất lớn?
Phương pháp giải:
a) Tìm công thức tổng quát của \({v_n}\) sau đó áp dụng giới hạn cơ bản: \(\lim \frac{1}{{{n^k}}} = 0\), với \(k\) nguyên dương bất kì.
b) Tính \({u_1},{u_2},{u_3},{u_4}\) rồi biểu diễn trên trục số.
Lời giải chi tiết:
a) \({v_n} = {u_n} - 2 = \frac{{2n + 1}}{n} - 2 = \frac{{2n + 1 - 2n}}{n} = \frac{1}{n}\).
Áp dụng giới hạn cơ bản với \(k = 1\), ta có: \(\lim {v_n} = \lim \frac{1}{n} = 0\).
b) \({u_1} = \frac{{2.1 + 1}}{1} = 3,{u_2} = \frac{{2.2 + 1}}{2} = \frac{5}{2},{u_3} = \frac{{2.3 + 1}}{3} = \frac{7}{3},{u_4} = \frac{{2.4 + 1}}{4} = \frac{9}{4}\)
Biểu diễn trên trục số:

Nhận xét: Điểm \({u_n}\) càng dần đến điểm 2 khi \(n\) trở nên rất lớn.
Tìm các giới hạn sau:
a) \(\lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right)\);
b) \(\lim \left( {\frac{{1 - 4n}}{n}} \right)\).
Phương pháp giải:
Bước 1: Đặt dãy số cần tính giới hạn là \({u_n}\), từ đó tìm \(a\) sao cho \(\lim \left( {{u_n} - a} \right) = 0\).
Bước 2: Áp dụng định lý giới hạn hữu hạn của dãy số: \(\lim {u_n} = a\) nếu \(\lim \left( {{u_n} - a} \right) = 0\).
Lời giải chi tiết:
a) Đặt \({u_n} = 2 + {\left( {\frac{2}{3}} \right)^n} \Leftrightarrow {u_n} - 2 = {\left( {\frac{2}{3}} \right)^n}\).
Suy ra \(\lim \left( {{u_n} - 2} \right) = \lim {\left( {\frac{2}{3}} \right)^n} = 0\)
Theo định nghĩa, ta có \(\lim {u_n} = 2\). Vậy \(\lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right) = 2\)
b) Đặt \({u_n} = \frac{{1 - 4n}}{n} = \frac{1}{n} - 4 \Leftrightarrow {u_n} - \left( { - 4} \right) = \frac{1}{n}\).
Suy ra \(\lim \left( {{u_n} - \left( { - 4} \right)} \right) = \lim \frac{1}{n} = 0\).
Theo định nghĩa, ta có \(\lim {u_n} = - 4\). Vậy \(\lim \left( {\frac{{1 - 4n}}{n}} \right) = - 4\)
Mục 1 của chương trình Toán 11 tập 1, Chân trời sáng tạo tập trung vào việc giới thiệu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, mở đầu cho chương trình Giải tích. Việc hiểu rõ về giới hạn sẽ giúp học sinh tiếp cận các khái niệm phức tạp hơn như đạo hàm và tích phân một cách dễ dàng hơn.
Giải:
Giải:
Ta có f(x) = (x2 - 1)/(x - 1) = (x - 1)(x + 1)/(x - 1). Với x ≠ 1, ta có f(x) = x + 1. Do đó, limx→1 f(x) = limx→1 (x + 1) = 1 + 1 = 2.
(Bài tập này yêu cầu học sinh xem đồ thị hàm số và xác định giá trị giới hạn dựa trên hành vi của đồ thị khi x tiến tới một điểm cụ thể.)
Để nắm vững kiến thức về giới hạn, các em nên làm nhiều bài tập khác nhau, từ cơ bản đến nâng cao. Ngoài ra, các em có thể tham khảo thêm các tài liệu học tập khác như sách tham khảo, video bài giảng, và các trang web học toán online uy tín.
Giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức hữu ích và giúp các em giải quyết các bài tập về giới hạn một cách hiệu quả. Chúc các em học tập tốt!