Bài 5 trang 85 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các hàm số lượng giác cơ bản, tính chất của chúng và các phương pháp giải phương trình lượng giác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 5 trang 85 SGK Toán 11 tập 2, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
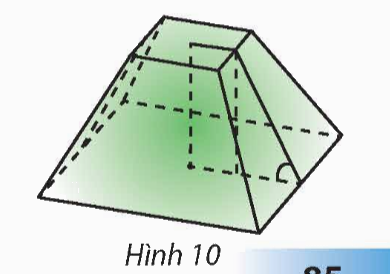
Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m.
Đề bài
Người ta định đào một cái hầm có dạng hình chóp cụt tứ giác đều có hai cạnh đáy là 14 m và 10 m. Mặt bên tạo với đáy nhỏ thành một góc nhị diện có số đo bằng 135°. Tính số mét khối đất cần phải di chuyển ra khỏi hầm.
Phương pháp giải - Xem chi tiết
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
‒ Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\).
Lời giải chi tiết
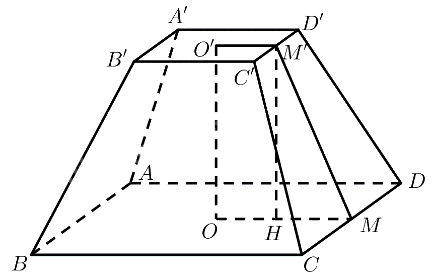
Mô hình hoá cái hầm bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 14,A'B' = 10\).
Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'\).
\(A'B'C'{\rm{D}}'\) là hình vuông \( \Rightarrow O'M' \bot C'{\rm{D}}'\).
\(CDD'C'\) là hình thang cân \( \Rightarrow MM' \bot C'D'\).
Vậy \(\widehat {MM'O'}\) là góc nhị diện giữa mặt bên và đáy nhỏ.
\( \Rightarrow \widehat {MM'O'} = {135^ \circ } \Rightarrow \widehat {M'MO} = {180^ \circ } - \widehat {MM'O'} = {45^ \circ }\).
Kẻ \(M'H \bot OM\left( {H \in OM} \right)\).
\(OHM'O'\) là hình chữ nhật
\( \Rightarrow OH = O'M' = 5,MH = OM - OH=7-5 = 2,M'H = OO' = MH.\tan {45^ \circ } = 2\).
Diện tích đáy lớn là: \(S = A{B^2} = {14^2} = 196\left( {{m^2}} \right)\).
Diện tích đáy bé là: \(S' = A'B{'^2} = {10^2} = 100\left( {{m^2}} \right)\).
Số mét khối đất cần phải di chuyển ra khỏi hầm là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.2\left( {196 + \sqrt {196.100} + 100} \right) = \frac{{872}}{3} \approx 290,67\left( {{m^3}} \right)\).
Bài 5 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình ôn tập chương 3 về hàm số lượng giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về hàm số lượng giác, bao gồm:
Dưới đây là lời giải chi tiết cho Bài 5 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo:
(Giả sử nội dung bài tập là: Giải các phương trình lượng giác sau: a) sin(x) = 1/2; b) cos(x) = -√3/2; c) tan(x) = 1; d) cot(x) = 0)
Phương trình sin(x) = 1/2 có nghiệm là:
Với k ∈ Z.
Phương trình cos(x) = -√3/2 có nghiệm là:
Với k ∈ Z.
Phương trình tan(x) = 1 có nghiệm là:
Với k ∈ Z.
Phương trình cot(x) = 0 có nghiệm là:
Với k ∈ Z.
Lưu ý: Khi giải phương trình lượng giác, cần kiểm tra lại các nghiệm để đảm bảo chúng thỏa mãn điều kiện xác định của phương trình.
Mở rộng: Để hiểu sâu hơn về hàm số lượng giác và phương pháp giải phương trình lượng giác, học sinh có thể tham khảo thêm các tài liệu sau:
Kết luận: Bài 5 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số lượng giác và phương pháp giải phương trình lượng giác. Việc nắm vững kiến thức này sẽ giúp học sinh tự tin giải các bài tập tương tự và đạt kết quả tốt trong các kỳ thi.
Xét phương trình sin(2x) = sin(x). Để giải phương trình này, ta sử dụng công thức sin(2x) = 2sin(x)cos(x). Khi đó, phương trình trở thành:
2sin(x)cos(x) = sin(x)
Chuyển vế và phân tích thành nhân tử, ta được:
sin(x)(2cos(x) - 1) = 0
Từ đó, ta có hai trường hợp:
Vậy nghiệm của phương trình sin(2x) = sin(x) là x = kπ, x = π/3 + k2π, x = -π/3 + k2π.