Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 10, 11 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học toán online hiệu quả, tiết kiệm thời gian và đạt kết quả tốt nhất.
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0). a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0).
a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
b) Xác định các điểm A’ và B’ trên đường tròn sao cho các góc lượng giác (OA; OA’), (OA, OB’) có số đo lần lượt là \(\pi \,\) và \( - \frac{\pi }{2}\)
Phương pháp giải:
Vẽ đường tròn rồi nhận biết từng góc
Lời giải chi tiết:
a) 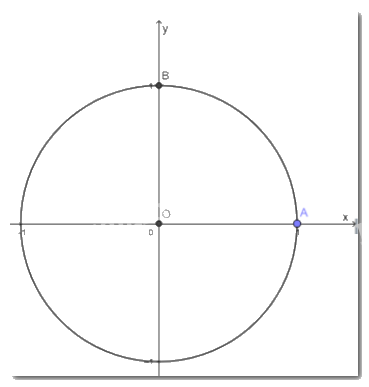
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
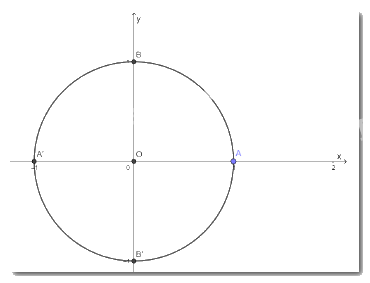
Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là:
a) \( - {1485^ \circ }\)
b) \(\frac{{19\pi }}{4}\)
Phương pháp giải:
Xác định góc lượng giác trên vòng tròn lượng giác.
Lời giải chi tiết:
a) Ta có \( - {1485^ \circ } = - {45^ \circ } + ( - 4){.360^ \circ }\). Vậy điểm biểu diễn góc lượng giác có số đo \( - {1485^ \circ }\)là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ IV sao cho \(\widehat {AMO} = {45^ \circ }\)
b) Ta có \(\frac{{19\pi }}{4} = \frac{{3\pi }}{4} + 4\pi \). Vậy điểm biểu diễn góc lượng giác có số đo \(\frac{{19\pi }}{4}\) là điểm N trên phần đường tròn lượng giác thuộc góc phần tư thứ II sao cho \(\widehat {AMO} = \frac{{3\pi }}{4}\).
Mục 3 trong SGK Toán 11 tập 1 chương trình Chân trời sáng tạo tập trung vào các kiến thức về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng trong chương trình Toán học, đặc biệt là khi các em bước vào học tập các kiến thức về đạo hàm và tích phân. Việc nắm vững kiến thức về giới hạn hàm số sẽ giúp các em hiểu rõ hơn về sự biến đổi của hàm số khi x tiến tới một giá trị nào đó.
Mục 3 trang 10, 11 SGK Toán 11 tập 1 Chân trời sáng tạo bao gồm các bài tập vận dụng kiến thức về giới hạn hàm số để giải quyết các bài toán cụ thể. Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu:
Hướng dẫn: Ta có thể phân tích tử thức thành nhân tử: x^2 - 4 = (x - 2)(x + 2). Sau đó, rút gọn biểu thức và tính giới hạn.
lim (x→2) (x^2 - 4) / (x - 2) = lim (x→2) (x - 2)(x + 2) / (x - 2) = lim (x→2) (x + 2) = 2 + 2 = 4
Hướng dẫn: Đây là một giới hạn lượng giác cơ bản. Các em có thể sử dụng định lý giới hạn đặc biệt: lim (x→0) sin(x) / x = 1
Hướng dẫn: Chia cả tử và mẫu cho x, ta được:
lim (x→∞) (2x + 1) / (x - 3) = lim (x→∞) (2 + 1/x) / (1 - 3/x) = (2 + 0) / (1 - 0) = 2
Ngoài SGK Toán 11 tập 1 Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng rằng với hướng dẫn chi tiết này, các em đã hiểu rõ hơn về cách giải bài tập mục 3 trang 10, 11 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!