Giải Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo

Bài 6 trang 24 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về các loại hàm số, tính đơn điệu, cực trị và ứng dụng để giải quyết các bài toán cụ thể.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 6 trang 24 SGK Toán 11 tập 1, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.

Chứng minh rằng tam giác ABC, ta có (sin A = sin B.cos C + sin C.cos B)

Đề bài

Chứng minh rằng tam giác ABC, ta có \(\sin A = \sin B.\cos C + \sin C.\cos B\)

Phương pháp giải - Xem chi tiết Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

Sử dụng định lý tổng 3 góc trong một tam giác bằng 180⁰ và áp dụng công thức cộng.

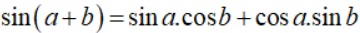
Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo 2

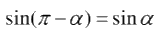
Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo 3

Lời giải chi tiết

Ta có: \(A + B + C = {180^0}\) (tổng 3 góc trong một tam giác)

\(\begin{array}{l} \Rightarrow A = {180^0} - \left( {B + C} \right)\\ \Leftrightarrow \sin A = \sin \left( {{{180}^0} - \left( {B + C} \right)} \right)\\ \Leftrightarrow \sin A = \sin \left( {B + C} \right) = \sin B.\cos C + \sin C.\cos B\end{array}\)

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo – hành trang không thể thiếu trong chuyên mục Bài tập Toán lớp 11 trên nền tảng môn toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo: Giải chi tiết và hướng dẫn

Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số và đồ thị. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Phần 1: Nội dung bài tập

Bài 6 yêu cầu học sinh thực hiện các nhiệm vụ sau:

Xác định tập xác định của hàm số.
Xét tính chẵn, lẻ của hàm số.
Tìm đạo hàm của hàm số.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
Giải các phương trình và bất phương trình liên quan đến hàm số.

Phần 2: Lời giải chi tiết

Để giải Bài 6 trang 24 SGK Toán 11 tập 1, chúng ta cần thực hiện các bước sau:

Bước 1: Xác định tập xác định của hàm số. Tập xác định của hàm số là tập hợp tất cả các giá trị của x sao cho hàm số có nghĩa.
Bước 2: Xét tính chẵn, lẻ của hàm số. Hàm số chẵn nếu f(-x) = f(x) với mọi x thuộc tập xác định. Hàm số lẻ nếu f(-x) = -f(x) với mọi x thuộc tập xác định.
Bước 3: Tìm đạo hàm của hàm số. Đạo hàm của hàm số là tốc độ thay đổi của hàm số theo biến x.
Bước 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số. Dựa vào đạo hàm, ta có thể xác định các khoảng đồng biến, nghịch biến, cực trị và vẽ đồ thị của hàm số.
Bước 5: Giải các phương trình và bất phương trình liên quan đến hàm số. Sử dụng kiến thức về hàm số và đồ thị để giải các phương trình và bất phương trình.

Phần 3: Ví dụ minh họa

Giả sử hàm số được xét là f(x) = x² + 2x + 1. Ta sẽ thực hiện các bước như sau:

Bước 1: Tập xác định: Tập xác định của hàm số là R.
Bước 2: Tính chẵn lẻ: f(-x) = (-x)² + 2(-x) + 1 = x² - 2x + 1 ≠ f(x) và f(-x) ≠ -f(x). Vậy hàm số không chẵn, không lẻ.
Bước 3: Đạo hàm: f'(x) = 2x + 2.
Bước 4: Khảo sát sự biến thiên: f'(x) = 0 khi x = -1. Hàm số nghịch biến trên (-∞, -1) và đồng biến trên (-1, +∞). Hàm số có cực tiểu tại x = -1, giá trị cực tiểu là f(-1) = 0.
Bước 5: Đồ thị: Đồ thị hàm số là một parabol có đỉnh tại (-1, 0) và mở lên trên.

Phần 4: Lưu ý khi giải bài tập

Khi giải Bài 6 trang 24 SGK Toán 11 tập 1, học sinh cần lưu ý những điều sau:

Nắm vững kiến thức về các loại hàm số, tính đơn điệu, cực trị và ứng dụng.
Thực hiện các bước giải một cách cẩn thận và chính xác.
Sử dụng đồ thị hàm số để kiểm tra lại kết quả.
Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.

Phần 5: Tổng kết

Bài 6 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và đồ thị. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin giải quyết bài tập này một cách hiệu quả.

Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!