Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải mục 1 trang 21 SGK Toán 11 tập 1 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) sau đây:
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) sau đây:
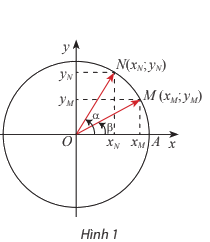
\(\overrightarrow {OM} .\overrightarrow {ON} = \left| {\overrightarrow {OM} } \right|.\left| {\overrightarrow {ON} } \right|.cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right)\)\( = cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right) = cos\left( {\alpha - \beta } \right)\)
\(\overrightarrow {OM} .\overrightarrow {ON} = {x_M}.{x_N} + {y_M}.{y_N}\)
Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.
Phương pháp giải:
Dựa vào hình vẽ và 2 công thức tính tích vô hướng để giải quyết
Lời giải chi tiết:
Ta có:
\(cos\left( {\alpha - \beta } \right) = {x_M}.{x_N} + {y_M}.{y_N} = cos\alpha .cos\beta + \sin \alpha .\sin \beta \)
\(cos\left( {\alpha + \beta } \right) = cos\left( {\alpha - \left( { - \beta } \right)} \right) = cos\alpha .cos\left( { - \beta } \right) + \sin \alpha .\sin \left( { - \beta } \right) = cos\alpha .cos\beta - \sin \alpha .\sin \beta \)
Tính \(\sin \frac{\pi }{{12}}\) và \(\tan \frac{\pi }{{12}}\)
Phương pháp giải:
Sử dụng công thức \(\sin \left( {a - b} \right) = \sin a\cos b - \cos asinb\).
\(\tan \alpha = \frac{{\sin \alpha }}{{cos\alpha }}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\sin \frac{\pi }{{12}} = \sin \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right) = \sin \frac{\pi }{3}cos\frac{\pi }{4} - cos\frac{\pi }{3}\sin \frac{\pi }{4}\\ = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 2 }}{2} - \frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 6 - \sqrt 2 }}{4}\\{\rm{cos}}\frac{\pi }{{12}} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\\\tan \frac{\pi }{{12}} = \frac{{\sin \frac{\pi }{{12}}}}{{{\rm{cos}}\frac{\pi }{{12}}}} = \frac{{\frac{{\sqrt 6 - \sqrt 2 }}{4}}}{{\frac{{\sqrt 6 + \sqrt 2 }}{4}}} = 2 - \sqrt 3 \end{array}\)
Mục 1 trang 21 SGK Toán 11 tập 1 - Chân trời sáng tạo thuộc chương trình học về hàm số và đồ thị. Đây là một phần quan trọng trong chương trình Toán 11, giúp học sinh hiểu rõ hơn về các khái niệm cơ bản của hàm số, cách xác định tập xác định, tập giá trị, và vẽ đồ thị hàm số.
Mục 1 trang 21 SGK Toán 11 tập 1 - Chân trời sáng tạo thường bao gồm các bài tập về:
Để giải các bài tập trong mục 1 trang 21 SGK Toán 11 tập 1 - Chân trời sáng tạo, bạn cần nắm vững các kiến thức cơ bản về hàm số, bao gồm:
Bài tập 1.1 yêu cầu xác định tập xác định của hàm số f(x) = √(x-2). Để giải bài tập này, ta cần tìm các giá trị của x sao cho biểu thức dưới dấu căn không âm. Tức là:
x - 2 ≥ 0
⇔ x ≥ 2
Vậy tập xác định của hàm số f(x) = √(x-2) là D = [2, +∞).
Bài tập 1.2 yêu cầu tìm tập giá trị của hàm số y = x2 - 4x + 3. Để tìm tập giá trị, ta có thể hoàn thiện bình phương:
y = x2 - 4x + 4 - 1
y = (x - 2)2 - 1
Vì (x - 2)2 ≥ 0 với mọi x, nên y ≥ -1.
Vậy tập giá trị của hàm số y = x2 - 4x + 3 là [ -1, +∞).
Bài tập 1.3 yêu cầu kiểm tra tính chẵn, lẻ của hàm số y = x3 + 2x. Để kiểm tra tính chẵn, lẻ, ta cần tính f(-x):
f(-x) = (-x)3 + 2(-x) = -x3 - 2x = -(x3 + 2x) = -f(x)
Vì f(-x) = -f(x) với mọi x, nên hàm số y = x3 + 2x là hàm số lẻ.
Ngoài SGK Toán 11 tập 1 - Chân trời sáng tạo, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng bài viết này đã giúp bạn giải mục 1 trang 21 SGK Toán 11 tập 1 - Chân trời sáng tạo một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!