Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4, trang 69, 70 và 71 của sách giáo khoa Toán 11 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
a) Cho hình lăng trụ (ABCDE.A'B'C'D'E') có cạnh bên (AA') vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?
a) Cho hình lăng trụ \(ABCDE.A'B'C'D'E'\) có cạnh bên \(AA'\) vuông góc với một mặt phẳng đáy (Hình 18a). Có nhận xét gì về các mặt bên của hình lăng trụ này?
b) Cho hình lăng trụ có đáy là đa giác đều và có cạnh bên vuông góc với một mặt phẳng đáy (Hình 18b). Có nhận xét gì các mặt bên của hình lăng trụ này?
c) Một hình lăng trụ nếu có đây là hình bình hành và có cạnh bên vuông góc với mặt phẳng đáy (Hình 18c) thì có bao nhiêu mặt là hình chữ nhật?
d) Một hình hộp nếu có đáy là hình chữ nhật và có cạnh bên vuông góc với mặt phẳng đáy (Hinh 18d) thì có bao nhiêu mặt là hình chữ nhật?
Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
a) Các mặt bên của hình lăng trụ này là hình chữ nhật vuông góc với mặt phẳng đáy.
b) Các mặt bên của hình lăng trụ này là hình chữ nhật vuông góc với mặt phẳng đáy.
c) Hình lăng trụ đó có 4 mặt bên là hình chữ nhật.
d) Hình lăng trụ đó có cả 6 mặt là hình chữ nhật.
Cho hình lăng trụ lục giác đều \(ABCDEF.A'B'C'D'E'F'\) có cạnh bên bằng \(h\) và cạnh đáy bằng \(a\). Tính \(A'C\) và \(A'D\) theo \(a\) và \(h\).
Phương pháp giải:
Sử dụng phép chiếu vuông góc.
Lời giải chi tiết:

Tam giác \(ABC\) có:
\(AC = \sqrt {A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}} = a\sqrt 3 \)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AC\)
\( \Rightarrow \Delta AA'C\) vuông tại \(A\)
\( \Rightarrow A'C = \sqrt {AA{'^2} + A{C^2}} = \sqrt {{h^2} + 3{{\rm{a}}^2}} \).
Gọi \(O\) là tâm lục giác đều \(ABC{\rm{DEF}}\).
\(\Delta OAB,\Delta OC{\rm{D}}\) đều \( \Rightarrow OA = O{\rm{D}} = AB = a \Rightarrow A{\rm{D}} = 2a\)
\(AA' \bot \left( {ABC{\rm{DEF}}} \right) \Rightarrow AA' \bot AD\)
\( \Rightarrow \Delta AA'D\) vuông tại \(A\)
\( \Rightarrow A'D = \sqrt {AA{'^2} + A{D^2}} = \sqrt {{h^2} + 4{{\rm{a}}^2}} \).
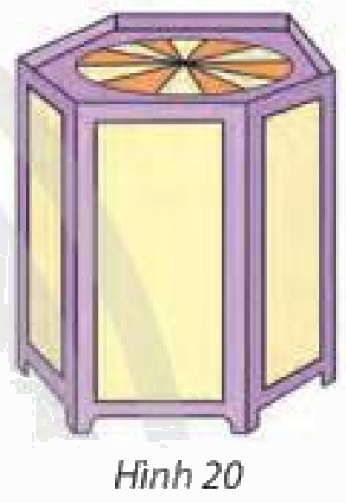
Một chiếc lồng đèn kéo quân có dạng hình lăng trụ lục giác đều với cạnh đáy bằng 10 cm và cạnh bên bằng 30 cm (Hình 20). Tính tổng diện tích các mặt bên của chiếc lồng đèn đó.

Phương pháp giải:
Tính diện tích 1 mặt. Tổng diện tích các mặt bên bằng 6 lần diện tích 1 mặt.
Lời giải chi tiết:
Diện tích một mặt bên của lồng đèn là: \(10.30 = 300\left( {c{m^2}} \right)\)
Tổng diện tích các mặt bên của chiếc lồng đèn đó là: \(300.6 = 1800\left( {c{m^2}} \right)\)
Mục 4 của SGK Toán 11 tập 2 - Chân trời sáng tạo tập trung vào các kiến thức về Đường thẳng và mặt phẳng trong không gian. Đây là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững các định nghĩa, tính chất và phương pháp chứng minh liên quan đến mối quan hệ giữa đường thẳng và mặt phẳng.
Để giải tốt các bài tập trong Mục 4, các em cần:
Bài 1: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết). Ví dụ: Để chứng minh hai đường thẳng song song, ta cần chỉ ra rằng hai đường thẳng đó nằm trong cùng một mặt phẳng và không có điểm chung. Sử dụng các tính chất về góc so le trong, góc đồng vị để chứng minh.
Bài 2: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết).
Bài 3: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết). Ví dụ: Để tính góc giữa hai đường thẳng, ta có thể sử dụng công thức cosin của góc giữa hai vectơ chỉ phương của hai đường thẳng.
Bài 4: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết).
Bài 5: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết). Ví dụ: Để chứng minh đường thẳng vuông góc với mặt phẳng, ta cần chứng minh đường thẳng đó vuông góc với mọi đường thẳng nằm trong mặt phẳng.
Bài 6: (Đề bài)... Lời giải: (Giải thích chi tiết từng bước, kèm theo hình vẽ minh họa nếu cần thiết).
Kiến thức về đường thẳng và mặt phẳng trong không gian có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, kỹ thuật, và đồ họa máy tính. Ví dụ, trong kiến trúc, việc xác định vị trí và hướng của các đường thẳng và mặt phẳng là rất quan trọng để thiết kế các công trình đảm bảo tính thẩm mỹ và an toàn.
Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc giải các bài tập Toán 11 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!