Bài 2 trang 81 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai tam giác cân (ABC) và (ABD) có đáy chung (AB) và không cùng nằm trong một mặt phẳng.
Đề bài
Cho hai tam giác cân \(ABC\) và \(ABD\) có đáy chung \(AB\) và không cùng nằm trong một mặt phẳng.
a) Chứng minh rằng \(AB \bot CD\).
b) Xác định đoạn vuông góc chung của \(AB\) và \(C{\rm{D}}\).
Phương pháp giải - Xem chi tiết
‒ Cách chứng minh hai đường thẳng vuông góc:
Cách 1: Chứng minh góc giữa chúng bằng \({90^ \circ }\).
Cách 2: Chứng minh đường thẳng này vuông góc với một mặt phẳng chứa đường thẳng kia.
‒ Cách dựng đoạn vuông góc chung của hai đường thẳng \(a\) và \(b\) vuông góc với nhau:
Bước 1: Xác định mặt phẳng \(\left( P \right)\) chứa \(b\) mà \(\left( P \right)\) vuông góc với \(a\).
Bước 2: Tìm giao điểm \(I = \left( P \right) \cap a\).
Bước 3: Kẻ \(IA \bot b\left( {A \in b} \right)\), chứng minh \(IA \bot a\). Khi đó \(d\left( {a,b} \right) = IA\).
Lời giải chi tiết
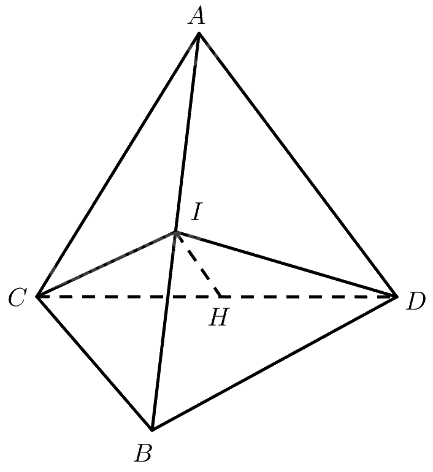
a) Gọi \(I\) là trung điểm của \(AB\)
\(\Delta ABC\) cân tại \(C\)\( \Rightarrow CI \bot AB\)
\(\Delta ABD\) cân tại \(D\)\( \Rightarrow DI \bot AB\)
\( \Rightarrow AB \bot \left( {C{\rm{D}}I} \right) \Rightarrow AB \bot C{\rm{D}}\)
b) Kẻ \(IH \bot C{\rm{D}}\left( {H \in C{\rm{D}}} \right)\)
\(AB \bot \left( {C{\rm{D}}I} \right) \Rightarrow AB \bot IH\)
Vậy \(IH\) là đoạn vuông góc chung của \(AB\) và \(C{\rm{D}}\).
Bài 2 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 2 yêu cầu tính đạo hàm của các hàm số sau:
a) y = x3 - 3x2 + 2x - 5
b) y = (x2 + 1)(x - 2)
c) y = (x2 + 3x) / (x + 1)
d) y = sin(2x) + cos(x)
Áp dụng công thức đạo hàm của tổng và hiệu, ta có:
y' = 3x2 - 6x + 2
Áp dụng quy tắc nhân, ta có:
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Áp dụng quy tắc chia, ta có:
y' = [(2x + 3)(x + 1) - (x2 + 3x)(1)] / (x + 1)2 = (2x2 + 5x + 3 - x2 - 3x) / (x + 1)2 = (x2 + 2x + 3) / (x + 1)2
Áp dụng công thức đạo hàm của hàm lượng giác, ta có:
y' = 2cos(2x) - sin(x)
Để giải các bài tập tương tự, bạn cần nắm vững các công thức đạo hàm cơ bản và các quy tắc đạo hàm như quy tắc nhân, quy tắc chia, quy tắc hợp. Ngoài ra, cần chú ý đến việc áp dụng đúng công thức đạo hàm của các hàm số lượng giác.
Ví dụ, để tính đạo hàm của hàm số y = (sin(x) + 1)2, bạn có thể áp dụng quy tắc hợp:
y' = 2(sin(x) + 1) * cos(x)
Đạo hàm có rất nhiều ứng dụng trong toán học và các lĩnh vực khác. Một số ứng dụng quan trọng của đạo hàm bao gồm:
Tìm cực trị của hàm số
Khảo sát hàm số
Tính tốc độ thay đổi của một đại lượng
Giải các bài toán tối ưu hóa
Việc hiểu rõ về đạo hàm và ứng dụng của nó là rất quan trọng để học tốt môn Toán 11 và chuẩn bị cho các kỳ thi quan trọng.
Để củng cố kiến thức về đạo hàm, bạn có thể luyện tập thêm các bài tập khác trong SGK Toán 11 tập 2 – Chân trời sáng tạo và các tài liệu tham khảo khác. giaitoan.edu.vn cung cấp nhiều bài tập giải chi tiết và hướng dẫn giải, giúp bạn tự tin hơn trong việc giải toán.
Hy vọng với lời giải chi tiết và hướng dẫn giải trên, bạn đã hiểu rõ về Bài 2 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo. Chúc bạn học tốt!