Chào mừng các em học sinh đến với lời giải chi tiết Bài 7 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo. Bài học này thuộc chương trình học Toán 11, tập trung vào các kiến thức về phép biến hóa affine.
giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3.
Đề bài
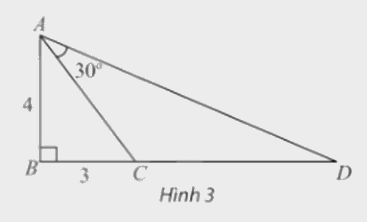
Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn \(\widehat {CAD} = {30^0}\). Tính \(\tan \widehat {BAD}\), từ đó tính độ dài cạnh CD.
Phương pháp giải - Xem chi tiết
Nhìn hình vẽ để tính \(\tan \widehat {BAC}\), sau đó áp dụng công thức cộng để tính \(\tan \widehat {BAD}\).
Lời giải chi tiết
Xét tam giác ABC vuông tại B có:
\(\tan \widehat {BAC} = \frac{3}{4}\)
Suy ra, \(\tan \widehat {BAD} = \tan \left( {\widehat {BAC} + \widehat {CAD}} \right) = \tan \left( {\widehat {BAC} + {{30}^0}} \right)\)
\( = \frac{{\tan \widehat {BAC} + \tan {{30}^0}}}{{1 - \tan \widehat {BAC}.\tan {{30}^0}}} = \frac{{\frac{3}{4} + \frac{{\sqrt 3 }}{3}}}{{1 - \frac{3}{4}.\frac{{\sqrt 3 }}{3}}} \approx 2,34\)
Xét tam giác vuông ABD vuông tại B có:
\(\begin{array}{l}BD = AB.\tan \widehat {BAD} = 4.2,34 \approx 9,36\\ \Rightarrow CD = BD - BC \approx 9,36 - 3 \approx 6,36\end{array}\)
Bài 7 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo yêu cầu chúng ta vận dụng kiến thức về phép biến hóa affine để giải quyết các bài toán cụ thể. Để hiểu rõ hơn về cách giải, chúng ta cùng đi vào phân tích từng phần của bài tập.
Bài tập này thường bao gồm việc xác định ma trận của phép biến hóa affine, tìm ảnh của một điểm hoặc một đường thẳng qua phép biến hóa affine, hoặc chứng minh một phép biến hóa là affine.
Để giải quyết bài tập này, chúng ta cần nắm vững các khái niệm và tính chất sau:
Giả sử chúng ta có một phép biến hóa affine f được xác định bởi ma trận:
A = [[2, 1], [1, 3]]
Và chúng ta muốn tìm ảnh của điểm M(1, 2) qua phép biến hóa f. Ta thực hiện phép nhân ma trận:
M' = A * M = [[2, 1], [1, 3]] * [[1], [2]] = [[4], [7]]
Vậy ảnh của điểm M(1, 2) qua phép biến hóa f là M'(4, 7).
Khi giải các bài tập về phép biến hóa affine, cần chú ý:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Bài 7 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp các em hiểu rõ hơn về phép biến hóa affine. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ nắm vững kiến thức và tự tin giải quyết các bài tập tương tự.
giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Phép biến hóa affine | Phép biến hóa bảo toàn tính thẳng hàng và tỉ số khoảng cách. |
| Ma trận của phép biến hóa affine | Biểu diễn phép biến hóa affine bằng một ma trận. |
| Bảng tóm tắt các khái niệm quan trọng. | |