Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 109, 110 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong môn Toán.
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10).
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
Phương pháp giải:
Để xác định vị trí tương đối của hai đường thẳng, ta dựa vào số điểm chung của hai đường thẳng đó.
Lời giải chi tiết:
Ta có: \(a\parallel \left( P \right) \Rightarrow \) Đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) không có điểm chung.
\(\left( P \right) \cap \left( Q \right) = b \Rightarrow b \subset \left( P \right)\)
Do đó hai đường thẳng \(a,b\) không có điểm chung.
Cho hai đường thẳng chéo nhau \(a,b\). Lấy một điểm \(M\) trên \(a\), vẽ đường thẳng \(b'\) đi qua \(M\) và song song với \(b\). Đặt \(\left( P \right)\) là mặt phẳng đi qua \(a,b'\).
a) Có nhận xét gì về mối liên hệ giữa \(b\) và \(\left( P \right)\).
b) Gọi \(\left( {P'} \right)\) là mặt phẳng chứa \(a\) và song song với \(b\). Có nhận xét gì về mối liên hệ giữa \(b'\) và \(\left( {P'} \right)\); \(\left( P \right)\) và \(\left( {P'} \right)\)?

Phương pháp giải:
Sử dụng hệ quả 1: Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Nếu qua điểm M thuộc \(\left( P \right)\) ta vẽ đường thẳng \(b\) song song với \(a\) thì \(b\) phải nằm trong \(\left( P \right)\).
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}b\parallel b'\\b' \subset \left( P \right)\end{array} \right\} \Rightarrow b\parallel \left( P \right)\)
b) Theo hệ quả 1, ta có:
\(\left. \begin{array}{l}b\parallel \left( {P'} \right)\\M \in b'\\b\parallel b'\end{array} \right\} \Rightarrow b' \subset \left( {P'} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}a \subset \left( P \right)\\a \subset \left( {P'} \right)\end{array} \right\} \Rightarrow a = \left( P \right) \cap \left( {P'} \right)\\\left. \begin{array}{l}b' \subset \left( P \right)\\b' \subset \left( {P'} \right)\end{array} \right\} \Rightarrow b' = \left( P \right) \cap \left( {P'} \right)\end{array}\)
Do đó \(a\) và \(b'\) đều là các đường thẳng chung của hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\).
Vì \(a\) và \(b'\) phân biệt, mà hai mặt phẳng phân biệt chỉ có duy nhất một đường thẳng chung nên \(\left( P \right) \equiv \left( {P'} \right)\).
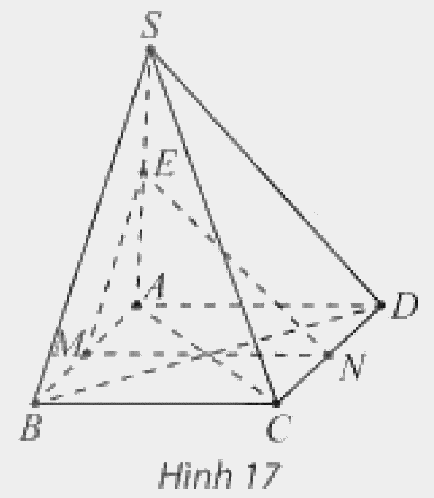
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và \(M,N,E\) lần lượt là trung điểm của các đoạn thẳng \(AB,CD,SA\) (Hình 17). Chứng minh rằng:
a) \(MN\) song song với hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SAD} \right)\);
b) \(SB\) và \(SC\) song song với mặt phẳng \(\left( {MNE} \right)\).

Phương pháp giải:
Để chứng minh đường thẳng song song với mặt phẳng, ta chứng minh đường thẳng đấy không nằm trong mặt phẳng và song song với một đường thẳng nằm trong mặt phẳng.
Lời giải chi tiết:
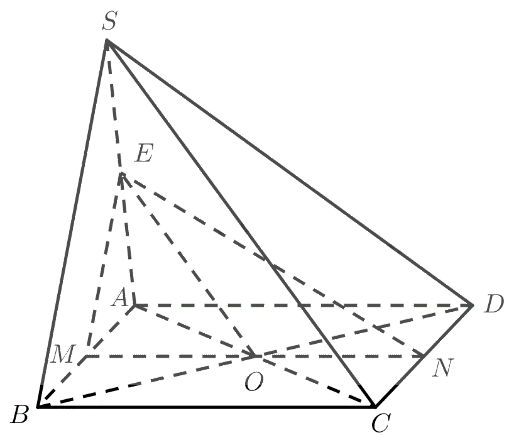
a) \(M\) là trung điểm của \(AB\)
\(N\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABCD\)
\( \Rightarrow MN\parallel A{\rm{D}}\parallel BC\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}MN\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SBC} \right)\\\left. \begin{array}{l}MN\parallel A{\rm{D}}\\A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SA{\rm{D}}} \right)\end{array}\)
b) \(M\) là trung điểm của \(AB\)
\(E\) là trung điểm của \(SA\)
\( \Rightarrow ME\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow ME\parallel SB\\ME \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SB\parallel \left( {MNE} \right)\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
\( \Rightarrow O\) là trung điểm của \(AC\) và \(O,M,N\) thẳng hàng
Mà \(E\) là trung điểm của \(SA\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel SC\\OE \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SC\parallel \left( {MNE} \right)\)
Làm thế nào để đặt cây thước kẻ \(a\) để nó song song các trang của một cuốn sách?
Phương pháp giải:
Sử dụng định lí 1: Nếu đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và song song với một đường thẳng \(b\) nào đó nằm trong \(\left( P \right)\) thì \(a\) song song với \(\left( P \right)\).
Lời giải chi tiết:
Để đặt cây thước kẻ \(a\) song song các trang của một cuốn sách, ta đặt nó song song với mép cuốn sách.
Mục 3 trong SGK Toán 11 tập 1 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết các bài toán thực tế. Việc hiểu rõ lý thuyết và phương pháp giải là yếu tố then chốt để hoàn thành tốt các bài tập này. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong mục 3 trang 109, 110, giúp các em học sinh củng cố kiến thức và nâng cao kỹ năng giải toán.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững nội dung chính của Mục 3. Thông thường, mục này sẽ đề cập đến các khái niệm, định lý và phương pháp liên quan đến một chủ đề cụ thể trong chương trình Toán 11. Ví dụ, nó có thể là về hàm số bậc hai, phương trình bậc hai, hoặc các chủ đề khác tùy thuộc vào chương trình học.
Để giúp các em hiểu rõ hơn về cách giải bài tập, chúng ta sẽ xem xét một ví dụ minh họa:
Ví dụ: (Nêu một bài tập cụ thể và giải chi tiết từng bước)
Ngoài việc giải các bài tập trong SGK, các em có thể tìm hiểu thêm về các chủ đề liên quan thông qua các nguồn tài liệu khác như sách tham khảo, bài giảng trực tuyến, hoặc các trang web học toán uy tín. Việc mở rộng kiến thức sẽ giúp các em hiểu sâu hơn về môn Toán và có khả năng giải quyết các bài toán phức tạp hơn.
Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 3 trang 109, 110 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Tóm tắt lời giải) |
| Bài 2 | (Tóm tắt lời giải) |