Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 5 trang 77, 78 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học toán online hiệu quả, tiết kiệm thời gian và đạt kết quả tốt nhất.
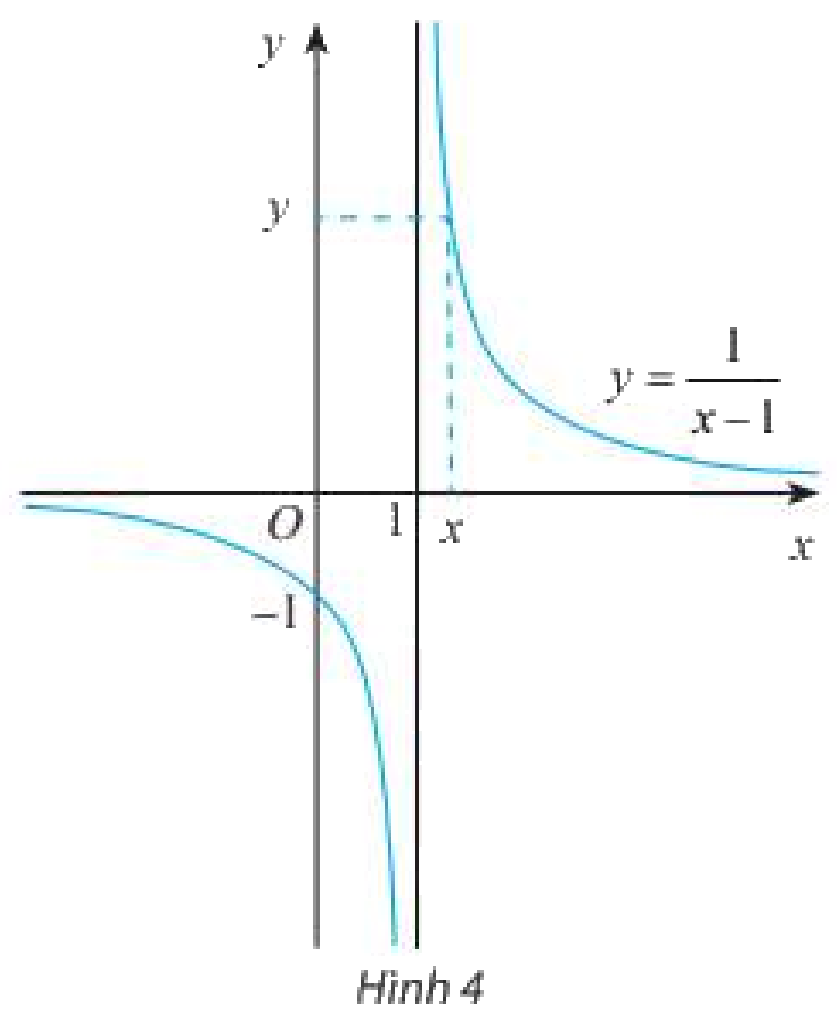
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\) có đồ thị như Hình 4.
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\) có đồ thị như Hình 4.
a) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên phải?
b) Tìm các giá trị còn thiếu trong bảng sau:

Từ đồ thị và bảng trên, có nhận xét gì về giá trị \(f\left( x \right)\) khi \(x\) dần tới 1 phía bên trái?
Phương pháp giải:
Để điền giá trị vào bảng, ta thay giá trị của \(x\) vào hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\).
Lời giải chi tiết:
a)
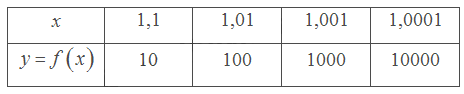
Giá trị \(f\left( x \right)\) trở nên rất lớn khi \(x\) dần tới 1 phía bên phải.
b)

Giá trị \(f\left( x \right)\) trở nên rất bé khi \(x\) dần tới 1 phía bên trái.
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}}\);
b) \(\mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right)\).
Phương pháp giải:
Bước 1: Đưa hàm số \(f\left( x \right)\) về tích của hai hàm số, trong đó một hàm số có giới hạn hữu hạn, còn một hàm số có giới hạn vô cực.
Bước 2: Áp dụng quy tắc xét dấu để tính giới hạn của tích.
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}} = \mathop {\lim }\limits_{x \to {3^ - }} \left( {2x} \right).\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}}\)
Ta có: \(\mathop {\lim }\limits_{x \to {3^ - }} \left( {2x} \right) = 2\mathop {\lim }\limits_{x \to {3^ - }} x = 2.3 = 6;\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}} = - \infty \)
\( \Rightarrow \mathop {\lim }\limits_{x \to {3^ - }} \frac{{2x}}{{x - 3}} = - \infty \)
b) \(\mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right) = \mathop {\lim }\limits_{x \to + \infty } x\left( {3 - \frac{1}{x}} \right) = \mathop {\lim }\limits_{x \to + \infty } x.\mathop {\lim }\limits_{x \to + \infty } \left( {3 - \frac{1}{x}} \right)\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } x = + \infty ;\mathop {\lim }\limits_{x \to + \infty } \left( {3 - \frac{1}{x}} \right) = \mathop {\lim }\limits_{x \to + \infty } 3 - \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 3 - 0 = 3\)
\( \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {3x - 1} \right) = + \infty \)
Xét tình huống ở đầu bài học. Gọi \(x\) là hoành độ điểm \(H\). Tính diện tích \(S\left( x \right)\) của hình chữ nhật \(OHMK\) theo \(x\). Diện tích này thay đổi như thế nào khi \(x \to {0^ + }\) và khi \(x \to + \infty \).
Phương pháp giải:
− Để tính diện tích \(S\left( x \right)\), ta tìm độ dài \(OH\) và \(OK\) rồi áp dụng công thức tính diện tích hình chữ nhật.
− Để xác định xem diện tích \(S\left( x \right)\) thay đổi như thế nào khi \(x \to {0^ + }\) và khi \(x \to + \infty \), ta tính giới hạn \(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right)\) và \(\mathop {\lim }\limits_{x \to + \infty } S\left( x \right)\).
Lời giải chi tiết:
Giả sử điểm \(M\) có hoành độ là \(x\).
Độ dài \(OH\) là hoành độ của điểm \(M\). Vậy \(OH = x\).
Độ dài \(OK\) là tung độ của điểm \(M\). Vậy \(OK = \frac{1}{{{x^2}}}\).
\(S\left( x \right) = OH.OK = x.\frac{1}{{{x^2}}} = \frac{1}{x}\).
\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = + \infty \). Vậy diện tích \(S\left( x \right)\) trở nên rất lớn khi \(x \to {0^ + }\).
\(\mathop {\lim }\limits_{x \to + \infty } S\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\). Vậy diện tích \(S\left( x \right)\) dần về 0 khi \(x \to + \infty \).
Mục 5 của chương trình Toán 11 tập 1 Chân trời sáng tạo tập trung vào việc nghiên cứu về phép biến hình. Cụ thể, các em sẽ được làm quen với các khái niệm như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để hiểu sâu hơn về hình học và các ứng dụng của nó trong thực tế.
Bài tập mục 5 trang 77, 78 SGK Toán 11 tập 1 Chân trời sáng tạo bao gồm các dạng bài tập khác nhau, từ việc xác định các yếu tố của phép biến hình đến việc chứng minh tính chất của các hình biến hình. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu các em xác định ảnh của một điểm hoặc một hình qua phép tịnh tiến. Để giải bài tập này, các em cần hiểu rõ định nghĩa của phép tịnh tiến và cách thực hiện phép tịnh tiến trên mặt phẳng tọa độ.
Bài tập này yêu cầu các em xác định ảnh của một điểm hoặc một hình qua phép quay. Để giải bài tập này, các em cần hiểu rõ định nghĩa của phép quay và cách thực hiện phép quay trên mặt phẳng tọa độ.
Bài tập này yêu cầu các em xác định ảnh của một điểm hoặc một hình qua phép đối xứng trục. Để giải bài tập này, các em cần hiểu rõ định nghĩa của phép đối xứng trục và cách thực hiện phép đối xứng trục trên mặt phẳng tọa độ.
Bài tập này yêu cầu các em xác định ảnh của một điểm hoặc một hình qua phép đối xứng tâm. Để giải bài tập này, các em cần hiểu rõ định nghĩa của phép đối xứng tâm và cách thực hiện phép đối xứng tâm trên mặt phẳng tọa độ.
Phép biến hình có rất nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực như:
Để học tốt môn Toán 11, các em cần:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả này, các em sẽ tự tin hơn trong quá trình học tập môn Toán 11. Chúc các em học tốt!