Chào mừng bạn đến với bài học về Lý thuyết Biến cố hợp và quy tắc cộng xác suất trong chương trình Toán 11 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và các công cụ cần thiết để giải quyết các bài toán liên quan đến xác suất.
Chúng ta sẽ cùng nhau khám phá định nghĩa biến cố hợp, các tính chất của nó, và đặc biệt là quy tắc cộng xác suất – một công cụ vô cùng quan trọng trong việc tính toán xác suất của các biến cố phức tạp.
1. Biến cố hợp Cho hai biến cố A và B.
1. Biến cố hợp
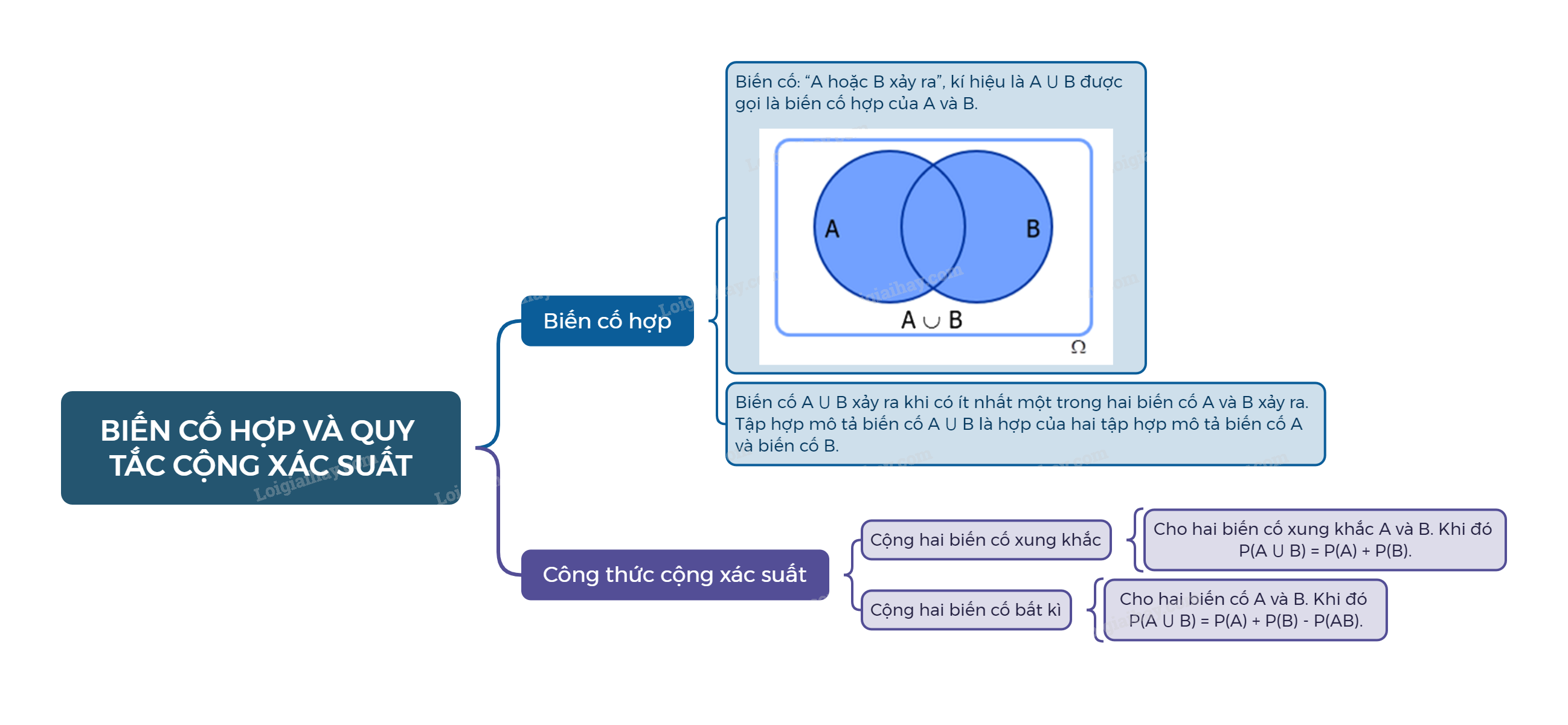
Cho hai biến cố A và B. Biến cố: “A hoặc B xảy ra”, kí hiệu là \(A \cup B\) được gọi là biến cố hợp của A và B.
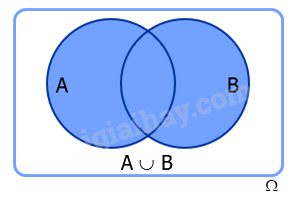
Chú ý: Biến cố \(A \cup B\) xảy ra khi có ít nhất một trong hai biến cố A và B xảy ra. Tập hợp mô tả biến cố \(A \cup B\) là hợp của hai tập hợp mô tả biến cố A và biến cố B.
2. Công thức cộng xác suất
Quy tắc cộng cho hai biến cố xung khắc:
Cho hai biến cố xung khắc A và B. Khi đó \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).
Quy tắc cộng cho hai biến cố bất kì:
Cho hai biến cố A và B. Khi đó \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\).
Trong chương trình Toán 11, phần xác suất đóng vai trò quan trọng trong việc rèn luyện tư duy logic và khả năng giải quyết vấn đề. Một trong những khái niệm cơ bản và thường xuyên xuất hiện trong các bài toán là biến cố hợp và quy tắc cộng xác suất. Bài viết này sẽ trình bày chi tiết về lý thuyết này, kèm theo các ví dụ minh họa để giúp bạn hiểu rõ hơn.
Định nghĩa: Cho hai biến cố A và B. Biến cố hợp của A và B, ký hiệu là A ∪ B, là biến cố xảy ra khi ít nhất một trong hai biến cố A hoặc B xảy ra.
Ví dụ: Tung một con xúc xắc sáu mặt.
Quy tắc cộng xác suất là công cụ quan trọng để tính xác suất của biến cố hợp. Có hai trường hợp:
Hai biến cố A và B được gọi là xung khắc nếu chúng không thể xảy ra đồng thời, tức là A ∩ B = ∅ (tập rỗng). Khi đó, xác suất của biến cố hợp A ∪ B được tính như sau:
P(A ∪ B) = P(A) + P(B)
Ví dụ: Tung một đồng xu.
Nếu hai biến cố A và B không xung khắc (tức là có thể xảy ra đồng thời), thì xác suất của biến cố hợp A ∪ B được tính như sau:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Trong đó, P(A ∩ B) là xác suất của biến cố giao của A và B (biến cố xảy ra đồng thời cả A và B).
Ví dụ: Rút một lá bài từ bộ bài 52 lá.
Bài 1: Một hộp chứa 5 quả bóng đỏ và 3 quả bóng xanh. Lấy ngẫu nhiên 2 quả bóng. Tính xác suất để lấy được ít nhất một quả bóng đỏ.
Giải: Gọi A là biến cố lấy được ít nhất một quả bóng đỏ. Khi đó, biến cố đối của A là Ac: lấy được cả hai quả bóng xanh.
P(Ac) = C(3,2) / C(8,2) = 3/28
P(A) = 1 - P(Ac) = 1 - 3/28 = 25/28
Lý thuyết này có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Lý thuyết Biến cố hợp và quy tắc cộng xác suất là nền tảng quan trọng trong học phần xác suất thống kê. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán xác suất một cách hiệu quả và áp dụng vào thực tế một cách linh hoạt. Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và nâng cao kỹ năng giải quyết vấn đề.