Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 66 và 67 sách giáo khoa Toán 11 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Từ một điểm (O) vẽ hai tia (Ox) và (Oy) lần lượt vuông góc với hai bức tường trong phòng. Đo góc (xOy).
Từ một điểm \(O\) vẽ hai tia \(Ox\) và \(Oy\) lần lượt vuông góc với hai bức tường trong phòng. Đo góc \(xOy\).
Phương pháp giải:
Thực hành đo góc và trả lời câu hỏi.
Lời giải chi tiết:
\(\widehat {xOy} = {90^ \circ }\).
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\) điểm \(M\) không thuộc \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(H\) và \(K\) lần lượt là hình chiếu vuông góc của \(M\) lên \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(O\) là giao điểm của \(d\) và \(\left( {MHK} \right)\) (Hình 8).

a) Giả sử \(\left( P \right) \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tìm trong \(\left( P \right)\) đường thẳng vuông góc với \(\left( Q \right)\).
b) Giả sử \(\left( P \right)\) chứa đường thẳng \(a\) với \(a \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tính góc giữa \(\left( P \right)\) và \(\left( Q \right)\).
Phương pháp giải:
Sử dụng định nghĩa: Góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) là góc giữa hai đường thẳng lần lượt vuông góc với \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot OH\\MK \bot \left( Q \right) \Rightarrow MK \bot OK\\\left( {\left( P \right),\left( Q \right)} \right) = {90^ \circ } \Rightarrow \left( {MH,MK} \right) = {90^ \circ } \Rightarrow MH \bot MK\end{array}\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HMK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
Trong \(\left( P \right)\) có đường thẳng \(OH\) vuông góc với \(\left( Q \right)\).
b) Ta có:
\(\left. \begin{array}{l}a \bot \left( Q \right) \Rightarrow a \bot OK\\MH \bot \left( P \right) \Rightarrow MH \bot a\end{array} \right\} \Rightarrow MH\parallel OK\)
Lại có \(MH \bot \left( P \right)\). Vậy \(OK \bot \left( P \right) \Rightarrow OK \bot OH\)
Tứ giác \(MHOK\) có \(\widehat {MHO} = \widehat {MK{\rm{O}}} = \widehat {HOK} = {90^ \circ }\).
Vậy tứ giác \(MHOK\) là hình chữ nhật.
\(\left( {\left( P \right),\left( Q \right)} \right) = \left( {MH,MK} \right) = \widehat {HMK} = {90^ \circ }\).
Cho hình chóp \(S.ABCD\) có các cạnh bên bằng nhau và đáy là hình vuông. Chứng minh rằng:
a) \(\left( {SAC} \right) \bot \left( {ABCD} \right)\);
b) \(\left( {SAC} \right) \bot \left( {SBD} \right)\).
Phương pháp giải:
Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.
Lời giải chi tiết:

a) Gọi \(O = AC \cap B{\rm{D}}\).
Tam giác \(SAC\) cân tại \(S \Rightarrow SO \bot AC\)
Tam giác \(SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow SO \bot \left( {ABCD} \right)\\SO \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow \left( {SAC} \right) \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(SO \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\\AC \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow \left( {SAC} \right) \bot \left( {SB{\rm{D}}} \right)\)
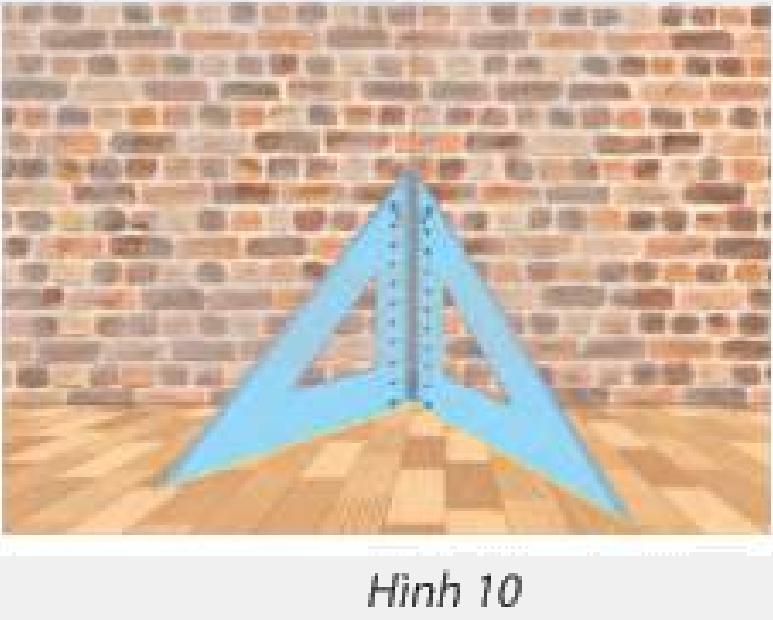
Mô tả cách kiểm tra một bức tường vuông góc với mặt sàn bằng hai cái êke trong Hình 10.

Phương pháp giải:
Sử dụng định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Lời giải chi tiết:
Đặt êke sao cho hai cạnh góc vuông của hai êke chạm nhau tạo thành một đường thẳng, hai cạnh còn lại của hai êke sát với mặt sàn.
Nếu đường thẳng đó nằm sát với bức tường thì bức tường vuông góc với mặt sàn.
Mục 2 của SGK Toán 11 tập 2 chương trình Chân trời sáng tạo tập trung vào các kiến thức về phép biến hình. Cụ thể, các em sẽ được làm quen với các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để học tập các kiến thức hình học nâng cao hơn trong chương trình.
Các bài tập trong mục 2 trang 66 và 67 SGK Toán 11 tập 2 yêu cầu học sinh vận dụng các kiến thức về phép biến hình để giải quyết các bài toán thực tế. Các bài tập thường bao gồm:
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 66 và 67 SGK Toán 11 tập 2:
Cho điểm A(1; 2) và phép tịnh tiến theo vectơ v = (3; -1). Tìm ảnh A' của điểm A qua phép tịnh tiến đó.
Lời giải:
Áp dụng công thức phép tịnh tiến: A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b)
Ta có: A'(1 + 3; 2 - 1) = A'(4; 1)
Vậy, ảnh A' của điểm A qua phép tịnh tiến theo vectơ v là A'(4; 1).
Cho đường thẳng d: x + 2y - 3 = 0 và phép quay tâm O(0; 0) góc -90°. Tìm ảnh d' của đường thẳng d qua phép quay đó.
Lời giải:
Để tìm ảnh của đường thẳng d qua phép quay tâm O góc -90°, ta cần tìm hai điểm thuộc d và tìm ảnh của chúng qua phép quay. Sau đó, ta tìm phương trình đường thẳng đi qua hai điểm ảnh này.
Chọn hai điểm A(1; 1) và B(3; 0) thuộc đường thẳng d.
Ảnh của điểm A(1; 1) qua phép quay tâm O góc -90° là A'(1; -1).
Ảnh của điểm B(3; 0) qua phép quay tâm O góc -90° là B'(0; -3).
Phương trình đường thẳng d' đi qua hai điểm A'(1; -1) và B'(0; -3) là: (y + 1) / (x - 1) = (-3 + 1) / (0 - 1) = 2
=> y + 1 = 2(x - 1) => y + 1 = 2x - 2 => 2x - y - 3 = 0
Vậy, ảnh d' của đường thẳng d qua phép quay tâm O góc -90° là 2x - y - 3 = 0.
Để học tốt môn Toán 11, các em cần:
Hy vọng với lời giải chi tiết và những chia sẻ trên, các em sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 66, 67 SGK Toán 11 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!