Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 5 trang 117, 118, 119 sách giáo khoa Toán 11 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Hình dạng của các đô vật như hộp phân, lồng đèn, hộp quà, lăng kính có đặc điểm gì giống nhau?
Hình dạng của các đô vật như hộp phân, lồng đèn, hộp quà, lăng kính có đặc điểm gì giống nhau?
Phương pháp giải:
Quan sát hình vẽ, tìm ra các đặc điểm chung.
Lời giải chi tiết:
Các hình trên đều có một cặp mặt phẳng đối diện song song với nhau.
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình bình hành. Chứng minh rằng:
a) Bốn mặt bên và mặt đáy còn lại của hình lăng trụ là các hình bình hành;
b) Các mặt \(AA'C'C\) và \(BB'D'D\)là hình bình hành
c) Bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.
Phương pháp giải:
‒ Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.
‒ Sử dụng tính chất của hình lăng trụ.
‒ Sử dụng tính chất của hình bình hành.
Lời giải chi tiết:

a) Vì \(ABCD.A'B'C'D'\) là hình lăng trụ nên có:
‒ Hai đáy \(ABCD\) và \(A'B'C'D'\) bằng nhau và là hình bình hành.
‒ Các mặt bên \(AA'B'B,AA'D'D,BB'C'C,CC'D'D\) là các hình bình hành.
b) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {AA'C'C} \right) \cap \left( {ABC{\rm{D}}} \right) = AC\\\left( {AA'C'C} \right) \cap \left( {A'B'C'D'} \right) = A'C'\end{array} \right\} \Rightarrow AC\parallel A'C'\)
Mà \(AA'\) và \(CC'\) là các cạnh bên của hình lăng trụ nên \(AA'\parallel CC'\)
Vậy \(AA'C'C\) là hình bình hành.
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {BB'D'D} \right) \cap \left( {ABC{\rm{D}}} \right) = B{\rm{D}}\\\left( {BB'D'D} \right) \cap \left( {A'B'C'D'} \right) = B'D'\end{array} \right\} \Rightarrow B{\rm{D}}\parallel B'D'\)
Mà \(BB'\) và \(DD'\) là các cạnh bên của hình lăng trụ nên \(BB'\parallel DD'\)
Vậy \(BB'D'D\) là hình bình hành.
c) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = C{\rm{D}}\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {A'B'C'D'} \right) = A'B'\end{array} \right\} \Rightarrow C{\rm{D}}\parallel A'B'\left( 1 \right)\)
\(ABC{\rm{D}}\) là hình bình hành nên \(AB = CD\)
\(AA'B'B\) là hình bình hành nên \(AB = A'B'\)
Vậy \(A'B' = CD\left( 2 \right)\)
Từ (1) và (2) suy ra \(A'B'C{\rm{D}}\) là hình bình hành
\( \Rightarrow A'C,B'D\) cắt nhau tại trung điểm của mỗi đường.
Chứng minh tương tự ta có:
+ \(ABC'D'\) là hình bình hành nên \(AC',B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
+ \(A'BCD'\) là hình bình hành nên \(A'C,B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
Do đó bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.
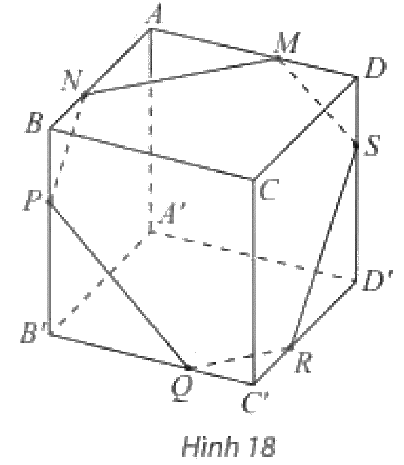
Cho hình hộp \(ABCD.A'B'C'D'\) và một mặt phẳng \(\left( \alpha \right)\) cắt các mặt của hình hộp theo các giao tuyến \(MN,NP,PQ{\rm{,}}QR,RS,SM\) như Hình 18. Chứng minh các cặp cạnh đối của lục giác \(MNPQRS\) song song với nhau.

Phương pháp giải:
Sử dụng định lí 3: Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau. Nếu \(\left( R \right)\) cắt \(\left( P \right)\) thì cắt \(\left( Q \right)\) và hai giao tuyến của chúng song song.
Lời giải chi tiết:
Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( \alpha \right) \cap \left( {A'B'C'D'} \right) = Q{\rm{R}}\end{array} \right\} \Rightarrow MN\parallel Q{\rm{R}}\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( \alpha \right) \cap \left( {AA'B'B} \right) = NP\\\left( \alpha \right) \cap \left( {CC'D'D} \right) = R{\rm{S}}\end{array} \right\} \Rightarrow NP\parallel R{\rm{S}}\)
\(\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( \alpha \right) \cap \left( {AA'D'D} \right) = M{\rm{S}}\\\left( \alpha \right) \cap \left( {BB'C'C} \right) = PQ\end{array} \right\} \Rightarrow M{\rm{S}}\parallel PQ\)
Tìm hình lăng trụ có thể lấy một mặt bất kì làm mặt đáy.
Phương pháp giải:
Sử dụng tính chất của hình lăng trụ, tìm các hình lăng trụ có các cặp mặt phẳng đối diện song song với nhau.
Lời giải chi tiết:
Hình lăng trụ có thể lấy một mặt bất kì làm mặt đáy là: Hình hộp, hình hộp chữ nhật, hình lập phương.
Mục 5 của SGK Toán 11 tập 1 - Chân trời sáng tạo tập trung vào các kiến thức về đạo hàm của hàm số. Cụ thể, các em sẽ được làm quen với các khái niệm như đạo hàm tại một điểm, đạo hàm của hàm số, quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số, và đạo hàm của một số hàm số cơ bản.
Đạo hàm của hàm số f(x) tại điểm x0, ký hiệu là f'(x0), là giới hạn của tỷ số \frac{f(x) - f(x_0)}{x - x_0} khi \Delta x tiến tới 0 (với \Delta x = x - x_0). Công thức tính đạo hàm tại một điểm:
f'(x_0) = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}
Để tính đạo hàm tại một điểm, các em cần thực hiện các bước sau:
Đạo hàm của hàm số f(x), ký hiệu là f'(x), là đạo hàm của f(x) tại mọi điểm x thuộc tập xác định của f(x). Công thức tổng quát:
f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}
Để tính đạo hàm của các hàm số phức tạp, chúng ta sử dụng các quy tắc sau:
Dưới đây là đạo hàm của một số hàm số cơ bản mà các em cần nắm vững:
| Hàm số f(x) | Đạo hàm f'(x) |
|---|---|
| x^n (n là số nguyên dương) | nx^{n-1} |
| \sin x | \cos x |
| \cos x | -\sin x |
| e^x | e^x |
| \ln x | \frac{1}{x} |
Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x^2 + 2x - 1
Áp dụng quy tắc đạo hàm của tổng/hiệu và quy tắc đạo hàm của lũy thừa, ta có:
f'(x) = 3(2x) + 2(1) - 0 = 6x + 2
Bài 1: Tính đạo hàm của hàm số f(x) = x^3 - 5x + 4
Bài 2: Tính đạo hàm của hàm số f(x) = \sin x + \cos x
Bài 3: Tính đạo hàm của hàm số f(x) = \frac{x^2 + 1}{x - 1}
Hy vọng với bài viết này, các em đã nắm vững kiến thức về đạo hàm và có thể tự tin giải các bài tập trong SGK Toán 11 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!